Назовем события 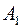 ,
, 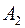 ,..,
,..,  равновозможными, если исходя из соображений симметрии, появление одного из них не является более предпочтительным, чем появление любого другого. Например, в опыте с бросанием правильной игральной кости следует считать события
равновозможными, если исходя из соображений симметрии, появление одного из них не является более предпочтительным, чем появление любого другого. Например, в опыте с бросанием правильной игральной кости следует считать события 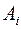 ,(
,( ) — выпадение
) — выпадение  очков, — равновозможными. Такие события называют еще равновероятными, так как вероятности их появления равны.
очков, — равновозможными. Такие события называют еще равновероятными, так как вероятности их появления равны.
Будем называть событие 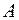 благоприятствующим событию В, если появление в эксперименте события А ведет к появлению события В.
благоприятствующим событию В, если появление в эксперименте события А ведет к появлению события В.
Пусть Ω конечно ( ), а все
), а все  равны между собой. Очевидно, что
равны между собой. Очевидно, что  . Все
. Все  образуют полную группу, они равновероятны и несовместны. Такие события называются случаями или шансами. В этой ситуации вероятность любого события
образуют полную группу, они равновероятны и несовместны. Такие события называются случаями или шансами. В этой ситуации вероятность любого события 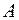 будет равна
будет равна
 ,
,
где  — число элементов
— число элементов  , входящих в множество
, входящих в множество 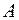 .
.
Это определение вероятности события 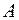 называется классическим. Его можно сформулировать еще так:
называется классическим. Его можно сформулировать еще так:
Определение 3.1. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных, несовместных элементарных исходов, образующих полную группу. Т.е. вероятность события А определяется формулой:
 , (3.1)
, (3.1)
где m – число элементарных исходов, благоприятствующих появлению события А, n – число всех возможных элементарных исходов испытания.
Из определения вероятности вытекают следующие ее свойства:
С1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию.
В этом случае  и, согласно формуле (3.1)
и, согласно формуле (3.1)
 .
.
С2. Вероятность невозможного события равна 0.
Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае 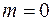 и следовательно
и следовательно
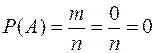 .
.
С3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных  исходов испытания. В этом случае
исходов испытания. В этом случае
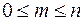

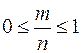

 .
.
События, вероятность которых очень мала (близка к нулю) или очень велика (близка к единице), называются соответственно практически невозможными или практически достоверными событиями.
Пример 3.1. Набирая номер телефона, абонент забыл последнюю цифру и набрал ее наугад. Найти вероятность того, что набрана нужная цифра.
Решение.
Пусть событие 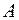 — набрана нужная цифра.
— набрана нужная цифра.
Абонент мог набрать любую из 10 цифр, поэтому, общее число возможных элементарных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможные (цифра набрана наудачу).
Благоприятствует событию 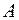 лишь один исход (нужная цифра лишь одна). Тогда искомая вероятность равна
лишь один исход (нужная цифра лишь одна). Тогда искомая вероятность равна
 .
.
Пример 3.2. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Решение. Обозначим через  событие – набраны две нужные цифры. Всего можно набрать столько пар различных цифр, сколько может быть составлено размещений из десяти цифр по 2, т.е.
событие – набраны две нужные цифры. Всего можно набрать столько пар различных цифр, сколько может быть составлено размещений из десяти цифр по 2, т.е.  . Таким образом, общее число возможных элементарных исходов равно 90. Эти исходы единственновозможные и равновозможные. Благоприятствует событию
. Таким образом, общее число возможных элементарных исходов равно 90. Эти исходы единственновозможные и равновозможные. Благоприятствует событию  лишь один исход.
лишь один исход.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
 .
.




