Почти всегда существуют ситуации, когда те или иные эксперименты или наблюдения могут быть произведены большое число раз в одинаковых условиях. Теорию вероятностей интересуют те эксперименты, результат которых может меняться от опыта к опыту.
Рассмотрим эксперимент, состоящий в подбрасывании монеты. Этот опыт имеет два исхода — выпадение герба или решки. До проведения эксперимента нельзя сказать, какой результат будет иметь место. Невозможно учесть все факторы, влияющие на положение монеты в момент падения. Точно так же невозможно, наблюдая за работой какого-то сложного механизма, определить заранее срок службы этого механизма. В этих ситуациях результаты отдельных экспериментов не обнаруживают какие-либо закономерности.
Однако если обратить внимание на последовательность таких испытаний, то наблюдается интересное явление — «средние» результаты обнаруживают устойчивость.
Введем понятие относительной частоты появления события, которая, наряду с вероятностью, принадлежит к основным понятиям теории вероятностей.
Определение 4.1. Относительной частотой (или просто частотой) появления события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.
Таким образом, относительная частота события 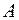 определяется формулой
определяется формулой
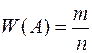 , (4.1)
, (4.1)
где 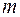 — число появлений события
— число появлений события 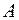 ,
, 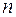 — общее число испытаний.
— общее число испытаний.
Определение относительной частоты лежит в основе определения статистической вероятности.
Пример 4.1. По цели произвели 32 выстрела, причем было зарегистрировано 20 попаданий. Найти относительную частоту попадания в цель.
Решение. Обозначим 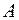 – попадание в цель. Согласно формуле (4.1), относительная частота поражения цели
– попадание в цель. Согласно формуле (4.1), относительная частота поражения цели
 .
.
Длительные наблюдения показали, что если в одинаковых условиях производятся опыты, в каждом из которых число испытаний достаточно велико, то относительная частота появления события обнаруживает свойство устойчивости, т.е. при достаточно больших 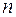 частоты устойчиво приближаются к некоторой постоянной величине. Эту постоянную величину и принимают за вероятность события. В этом суть статистического определения вероятности.
частоты устойчиво приближаются к некоторой постоянной величине. Эту постоянную величину и принимают за вероятность события. В этом суть статистического определения вероятности.
Определение 4.2. Вероятностью события в статистическом смысле называется число, относительно которого стабилизируется относительная частота появления события при неограниченном увеличении числа опытов, т.е., при.
Сопоставляя определение вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту — после опыта.
Пример 4.2. Многократно производились опыты с подбрасыванием правильной монеты, в которых подсчитывали появление герба. Результаты эксперимента приведены в таблице 4.1.
Таблица 4.1.
| Экспериментатор | Число бросаний | Число появлений герба | Относительная частота |
| Бюффон | 0,5069 | ||
| Пирсон | 0,5016 | ||
| Пирсон | 0,5005 |
Здесь относительные частоты незначительно отклоняются от числа 0,5, причем чем больше число испытаний, тем меньше отклонение относительной частоты. Например, при 4040 испытаниях отклонение равно 0, 0069, а при 24000 — лишь 0,0005
Приняв во внимание, что вероятность выпадения герба при бросании монеты равна 0,5, мы убеждаемся, что относительна частота колеблется около вероятности.
Статистическое определение вероятности связывают с именем Мизеса. Однако следует отметить недостатки такого определения вероятности. Прежде всего, последовательность частот  будет меняться при разных сериях экспериментов. Определить в этом случае строгий предельный переход
будет меняться при разных сериях экспериментов. Определить в этом случае строгий предельный переход  затруднительно. Кроме того, в нашем распоряжении имеется не вся последовательность, а лишь конечное число ее элементов. Получить всю последовательность невозможно.
затруднительно. Кроме того, в нашем распоряжении имеется не вся последовательность, а лишь конечное число ее элементов. Получить всю последовательность невозможно.






