Рассматривая классическое и статистическое определение вероятности, мы всегда предполагали, что число исходов опыта является конечным и все исходы равновозможные. Но часто встречаются такие испытания, для которых число возможных исходов бесконечно. В этом случае, если позволяют обстоятельства, используют следующую геометрическую интерпретацию.
Пусть имеется некоторая область 
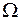(отрезок, плоская фигура, пространственная область), и в ней содержится другая область 
(рис. 5.1). Будем говорить, что область 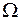имеет меру и обозначать ее через 
, понимая под этим длину, площадь, или объем области .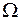
Аналогично и область имеет меру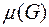 
, только в этом случае это будет ее длина, площадь или объем.
Производится испытание: в область 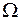наугад бросается точка и спрашивается: чему равна вероятность того, что точка попадет в область (событие А). При этом подразумевается, что брошенная точка может попасть в любую точку области Ω и вероятность попасть в какую-либо часть области, например в , пропорциональна мере этой части (длине, площади, объему) и не зависит от ее расположения и формы.
Определение 5.1. Геометрической вероятностью события A называется отношение меры области, благоприятствующей появлению события A, к мере всей области исходов:
. (5.1)
Пусть отрезок имеет длину 
, а его часть — длину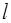 
, плоская фигура имеет площадь 
, а ее часть —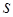 
, пространственная фигура имеет объем 
, а ее часть — 
. Тогда из формулы (5.1) получаем:
1. вероятность попадания точки на отрезок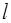
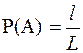; (5.2)
2. вероятность попадания точки в плоскую область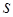
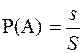; (5.3)
3. вероятность попадания точки в пространственную область
. (5.4)
Пример 5.1. На отрезке L длины 20 см помещен меньший отрезок 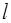длины 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
Решение.
За событие А обозначим утверждение: точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Тогда, согласно формуле (5.2) имеем
.
Ответ: 0,5.
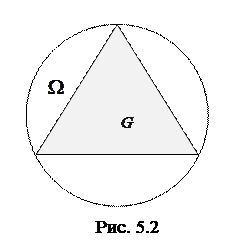
Пример 5.2. В круг радиуса R наудачу брошена точка. Найдите вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника.
Решение.
Обозначим за событие А – точка окажется внутри вписанного правильного треугольника (рис. 5.2). Тогда искомая вероятность равна отношению площади правильного треугольника к площади круга:
.
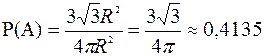Ответ: 
.
Пример 5.3. Шар 
помещен внутрь эллипсоида 
. Найти вероятность того, что поставленная наудачу внутри эллипсоида точка окажется внутри шара.
Решение. По определению геометрической вероятности искомая вероятность равна отношению объема эллипсоида (в который точка должна попасть) к объему шара (в которой точка ставится), т.е. 
.
Так как 
, а 
, то получаем
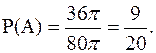
Ответ: 
