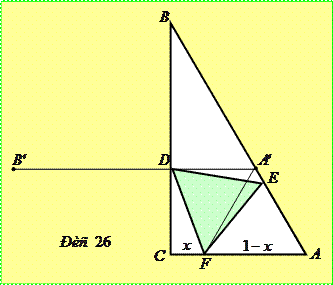
Задача 5.5.1. У прямокутний трикутник 
з гострим кутом 
та прямим кутом 
вписано правильний трикутник так, що його вершини лежать на різних сторонах даного трикутника. При якій умові сторона правильного трикутника буде найменшою?
Розв’язання. Нехай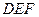 
– правильний трикутник, вписаний у даний трикутник (рис. 26). Вважатимемо 
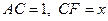. Тоді 
. Точку 
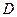можна розглядати, як результат повороту точки 
навколо точки 
на кут 
проти годинникової стрілки. Тоді точку 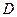можна одержати внаслідок перетину відрізків 
та 
, де - це образ відрізка 
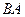при повороті на проти годинникової стрілки навколо центра повороту . Оскільки кут , то точка 
. Очевидно, що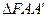 
– правильний і 
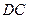. Знайдемо висоту 
у :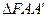 
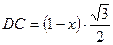. Із прямокутного трикутника 
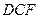сторона вписаного трикутника дорівнює 
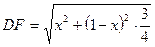. Розглянемо функцію 
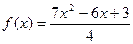. Вона набуває свого найменшого значення при 
= 
.
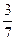Отже, якщо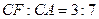 
, тобто 
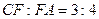, то вписаний правильний трикутник буде шуканий.
Задача 5.5.2. Всередині трикутника знайти точку 
, для якої сума квадратів відстаней від неї до сторін трикутника мінімальна.
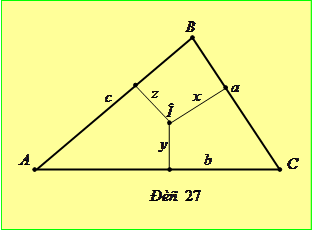Розв’язання. Нехай відстані від точки до сторін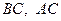 
, 
будуть відповідно 
(рис. 27). Тоді
,
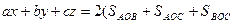де 
- площа даного трикутника. Сума квадратів відстаней від точки до сторін трикутника буде дорівнювати 
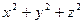. В силу нерівності Коші - Буняковського виконується співвідношення
,
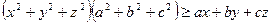причому знак рівності виконується при умові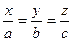 
. Одержуємо, що
.
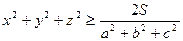Права частина є сталим числом. Тому ліва частина прийматиме найменше значення, коли виконується знак рівності, тобто при умові 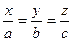. Із цих співвідношень та рівності 
остаточно дістаємо
.
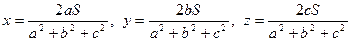Задача 5.5.3. Дано дві паралельні прямі та точка між ними. Побудувати прямокутний трикутник з вершиною прямого кута в точці та вершинами на заданих паралельних прямих, площа якого мінімальна.
Розв’язання. Проведемо через точку перпендикуляр до паралельних прямих (рис. 28). Нехай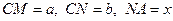 
. Трикутники 
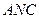і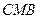 
подібні. Тому 
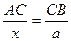або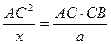 
, звідки 
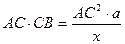. Оскільки 
і 
, то 
. Отже, площа буде найменшою, коли найменшою буде сума 
. Добуток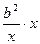 
є сталим числом 
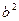, тому сума буде найменшою при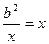 
, тобто при 
. Але якщ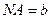о 
, то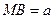 
. Тепер трикутник легко будується.
Задача 5.5.4. Знайти найкоротший відрізок, який ділить рівносторонній трикутник із стороною 
на дві рівновеликі фігури.
Розв’язання. Нехай трикутник рівносторонній із стороною . Позначимо шуканий відрізок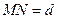 
. Нехай 
, 
(рис. 29). Тоді площа 
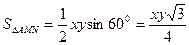. Оскільки площа всього трикутника дорівнює 
, то з умови отримуємо, що 
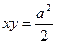або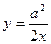 
. За теоремою косинусів 
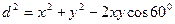або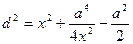 
. Очевидно, що відрізок 
буде найменшим, коли найменшим буде значення виразу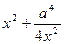 
. Добуток обох доданків є сталим і 
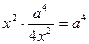, тому найменше значення суми буде при 
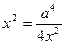, тобто при 
. При цьому значенні 
і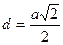 
.
Застосування похідної
Задача 5.6.1. У правильну чотирикутну піраміду з ребром основи і висотою 
вписана правильна чотирикутна призма так, що її нижня основа лежить всередині основи піраміди, а вершини верхньої основи – на бічних ребрах піраміди. Знайдіть найбільшу площу бічної поверхні таких призм.
Розв’язання. Нехай правильна чотирикутна призма вписана в піраміду так, як показано на рисунку 30. Нехай сторона основи призми дорівнює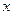 
, а її висота 
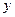.З подібності трикутників 
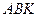та 
отримуємо 
, а з подібності трикутників 
та 
випливає співвідношення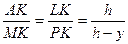 
. З пропорції 
знаходимо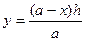 
. Оскільки площа бічної поверхні призми дорівнює 
, то маємо 
.
Одержаний квадратний відносно 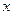тричлен з від’ємним старшим коефіцієнтом досягає свого найбільшого значення в точці 
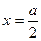. При цьому максимальна площа бічної поверхні буде 
.
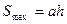Задача 5.6.2. Навколо правильної трикутної призми з об’ємом 
описаний циліндр. Знайдіть найменшу площу повної поверхні таких циліндрів.
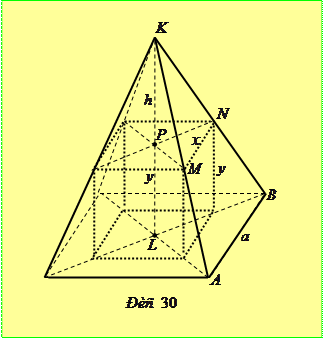
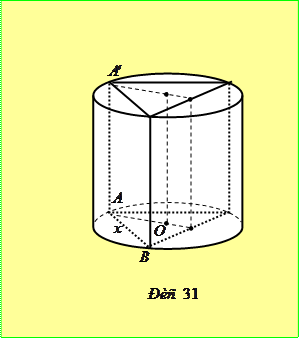Розв’язання. Нехай висота призми 
, сторона основи 
, радіус кола, описаного навколо основи 
(рис. 31). Оскільки радіус кола, описаного навколо правильного трикутника, дорівнює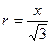 
, то, відповідно до умови, 
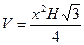, звідки 
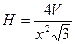. Тоді площа поверхні циліндра 
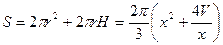. Розглянемо функцію 
, 
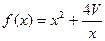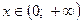. Оскільки її похідна 
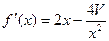перетворюється в 0 при 
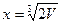і у цій точці функціяприймає, як легко встановити, найменше значення, то 
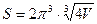є найменшим значенням площі поверхні циліндра.
У деяких випадках для знаходження найбільшого і найменшого значення при розв’язанні геометричних задач не завжди зрозуміло, в яких межах змінюється значення величини, яка нас цікавить. Тоді зручно цю величину виразити через інші величини.
Задача 5.6.3. Плоска фігура складається з прямокутника і рівностороннього трикутника. Визначити її розміри так, щоб при даному периметрі площа була найбільшою (у величину периметра не враховується спільна сторона прямокутника і трикутника).
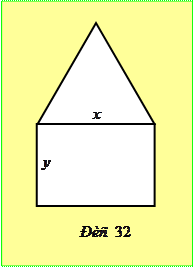Розв’язання. Нехай 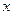– сторона трикутника, 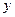– сторона прямокутника (рис. 32). Тоді периметр 
, звідки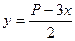 
.Очевидно, що площа всієї фігури буде
= 
=
= 
.
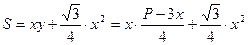
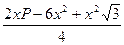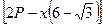Значення 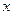, при якому площа буде найбільшою, визначаємо за допомогою похідної у виді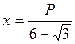 
. Тоді 
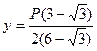. Це і є розміри фігури, при яких при заданому периметрі площа буде найбільшою.
Задача 5.6.4. Який із всіх рівнобедрених трикутників, вписаних у дане півколо так, щоб одна із рівних сторін лежала на діаметрі, а друга була б хордою, має найбільшу основу?
Розв’язання. Нехай шуканим є трикутник і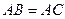 
, 
, 
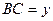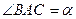(рис. 33), 
- радіус заданого півкола з діаметром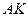 
.Проведемо 
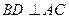. Нехай 
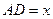. Тод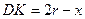і 
і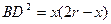 
. Тепер знаходимо, що 
. З прямокутного трикутника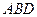 
отримуємо 
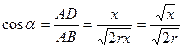, а із рівнобедреного трикутника за теоремою косинусів маємо 
.
Розглянемо функцію 
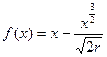, визначену на інтервалі 
. Оскільки її похідна 
перетворюється в 0 при 
і 
у цій точці приймає найбільше значення, то знайдене значення є шуканим та вказує, як побудувати трикутник.
