Відомо, що учні нерідко допускають помилки при формулюванні означення математичних понять. Виправляти їх найкраще за допомогою контр прикладів. До нижче поданих неправильних означень, які сформулював учень, наведіть можливі контр приклади: Середньою лінією трапеції називається лінія, що сполучає середини її бічних сторін. Відрізок прямої, що сполучає середини сторін трапеції, називається середньою лінією трапеції.
Які Ваші зауваження щодо поданих означень таких математичних об'єктів: Чотирикутник, у якого протилежні сторони рівні, називається паралелограмом. Ромбом називається чотирикутник, у якого протилежні сторони паралельні, а дві суміжні сторони рівні.
Ще й у 5-6 класах учні часто плутають, а точніше не можуть пояснити, чим відрізняються поняття "число" і "цифра". Допоможіть учням розібратися в смислі цих понять.
Пояснення про різницю між поняттями «число» і «цифра» я б провела за наступним планом:
– Цифри – це знаки, а числа це кількісна абстракція.
Для пояснення я б виклала на столі за допомогою магнітних цифр числа 9 і 14.
– Чим відрізняються запис числа 9 від запису числа 14?
Проведу аналогію із записом слова. За допомогою чого записуються слова? За допомогою літер – скаже дитина. А числа записуються за допомогою цифр. Число 9 записується за допомогою цифри 9 а ось число 14 за допомогою двох цифр 1 і 4. А скільки всього є цифр? – цифр всього 10: 0,1,2,3,4,5,6,7,8,9. Із допомогою цих цифр можна записати будь яке число.
Отже цифри – це одиниці рахунку від 0 до 9 (як і букви в алфавіті), а числа – складаються з цифр (як і слова складаються з букв).
Аналогія Цифри як і букви – це знаки, елементарну одиниці. Числа як і слова – це певна абстракція, яку придумали люди і зокрема числа виступають як міра кількості чогось.
31. Учень правильно відповів на запитання вчителя: " Які числа діляться на 2, а які - на 4?". На " зустрічне" запитання "Які числа діляться на 8?" учень сказав, що ті, які діляться на 2 й на 4. Чи згодні Ви з відповіддю учня? Відповідь обґрунтувати.
Так, у твоїх словах є істина, але давай ми розглянемо властивість подільності на число 8 і тоді ти зрозумієш у чому твоя помилка.
Вважаємо, що ми знаємо всі однозначні, двозначні та тризначні числа, що діляться на 8:
0; 8; 16; 24; 32;...; 992.
Таких чисел буде 1+1000:8–1=125.
Для довільного числа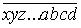 
, у якого чотири або більше цифр, можна записати рівність:
Наприклад, 123567=123×1000+567.
Число 1000 ділиться на 8 без остачі. Тому із властивості подільності: Якщо кожне з двох чисел a та b ділиться на c, то їх сума a + b ділиться на c.
та записаної рівності маємо таку достатню умову подільності на 8: якщо число, утворене трьома останніми цифрами, записаними в тому ж порядку, ділиться на 8, то число ділиться на 8.
Покажемо, що ця умова необхідна. Для цього запишемо отриману рівність у вигляді:
і використаємо властивість подільності: Якщо кожне з двох чисел a та b ділиться на c, то їх різниця a – b ділиться на c, згідно якої число 
ділиться на 8, якщо на 8 ділиться число .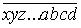
Таким чином, маємо ознаку подільності на 8:
для того, щоб число ділилося на 8, необхідно і досить, щоб ділилося на 8 тризначне число, утворене трьома останніми цифрами, записаними у тому порядку, в якому вони стоять у числі.
Зауваження. Зрозуміло, що кожне число, яке ділиться на 8, парне і ділиться на 4. Отже, маємо ще дві необхідні умови подільності на 8:
для того, щоб число ділилося на 8, необхідно, щоб воно було парне,
а також
для того, щоб число ділилося на 8, необхідно, щоб воно ділилося на 4.
Ці умови недостатні, тому що є числа, які діляться на 4 і не діляться на 8. Наприклад, 4; 12 та інші.
Думаю тепер у тебе не виникне хибної думки про те, які ж числа діляться на 8.
Наведіть приклади практичного використання основної властивості дробу і дайте формулювання цієї властивості.
Нагадаємо основну властивість частки: якщо ділене і дільник помножити на одне й те саме відмінне від нуля число, то частка від цього не зміниться. Оскільки звичайний дріб можна розглядати як частку від ділення, то цю властивість можна застосовувати і до звичайних дробів.
½= 2/4=4/8, в цій рівності з лівої частини одержимо праву, якщо чисельник і знаменник дробу помножимо на 2: 2/4=(2*2)/(4*2)=4/8.
Тепер розглянемо рівність 4/8=2/4: у цій рівності з лівої частини одержимо праву, якщо чисельник і знаменник дробу поділимо на 2, тобто 4/8= (4:2)/(8:2)=2/4.
Маємо основну властивість дробу:
Значення дробу не змінюється, якщо чисельник і знаменник дробу помножити або поділити на одне й те саме відмінне від нуля число.
Наприклад: 2/5=(2*3)/(5*3)=6/15;
14/20= (14:2)/(20:2)=7/10.
Використання:
а) Скорочення дробу
З рівності 2/5=6/15 випливає, що дроби 2/5 і 6/15 є різними записами одного й того самого числа. Оскільки 14/20=7/10, то ці дроби є також різними записами одного числа.
Ділення чисельника і знаменника дробу на одне й те саме натуральне число називається скороченням дробу. При цьому один дріб замінюють на інший, що дорівнює даному, але порівняно з ним має менші чисельник і знаменник.
Найбільшим числом на яке можна скоротити дріб, є найбільший спільний дільник чисельника і знаменника. Дріб 4/5 скоротити не можна. Такий дріб називають нескоротним. Чисельник і знаменник нескоротного дробу є взаємно простими числами.
б) Зведення дробу до нового знаменника
Використовуючи основну властивість дробу, дріб ¾ можна записати дробом зі знаменником 12, помноживши його чисельник і знаменник на3:
¾=(3*3)/(4*3)=9/12
Цей же дріб можна змінити дробом зі знаменником 20, помноживши його чисельник і знаменник на 5: ¾=(3*5)/(4*5)=15/20.
Нехай дріб ¾ потрібно звести до дробу зі знаменником 96. спочатку потрібно дізнатись, на яке натуральне число потрібно помножити 4, щоб отримати 96(якщо таке число існує). Для цього потрібно число 96 поділити на 4: 96/4=24. Тоді ¾=(3*24)/4*24)=72/96. Число 24 в цьому прикладі називається додатковим множником.
