Опишіть стандартний і нестандартний способи розв'язання завдання: спростити:

 

Описати стандартний і нестандартний способи розв'язання вправи: обчислити:.

 

Поясніть, що означають ці символи:,;,.

 

1. 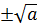, –Квадратний корінь з невід’ємного числа а().є числа і .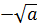

Квадратним коріенем з числа 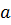називають число, квадрат якого дорівнює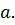

Наприклад: квадратний корінь із числа 4 є числа 2 і -2. Справді, .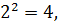

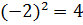2.. , - Арифметичний квадратний корінь з невід’ємного числа а ().є число .

Арифметичним квадраттним коренем з числа 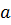називають невід’ємне число, квадрат якого дорівнює .

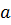Арифметичний квадратний корінь з числа 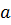позначають . Знак 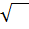називають знаком квадратного кореня або радикалом.

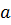Запис читають «квадратний корінь з ». Якщо 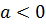, то вираз не має змісту.

Вираз, який стоїть під знаком радикала, називають підкореневим виразом. З означення арифметичного квадратного кореня випливає, що підкореневий вираз може набувати тільки невід’ємних значень.Дію знаходження арифметичного квадратного кореня з числа називають добуванням квадратного кореня.

Наприклад: 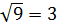, оскільки 3≥0 і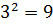

З означення арифметичного квадратного корення випливає, що при невід’ємних значеннях 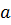справедлива рівність

У шкільному курсі математики вивчають такі тотожності, як формули скороченого множення. Стверджується, що кожну з цих тотожностей можна використати подвійно. В чому сенс цього твердження.

 

У 7 класі учні вивчають тотожні перетворення виразів такі як формули скороченого множення.

Формули скороченого множення застосовуються для тотожних перетворень, зокрема для розкладу многочленів на множники, для спрощення виразів, швидкого множення многочленів та для зведення многочленів до стандартного вигляду. Всі формули скороченого множення доводяться безпосередньо розкриттям дужок і зведенням подібних доданків.

Основними формулами якими учні повинні володіти такі:

Формули для квадратів

(a + b)² = a² + 2ab + b²– квадрат суми

(a + b)² = a² + 2ab + b²– квадрат різниці

a² – b² = (a – b)(a +b) – різниця квадратів

Формули для кубів

(a +b)³ =a³ +3a²b+ 3ab² +b³– куб суми

(a –b)³ =a³ – 3a²b + 3ab² –b³ - куб різниці

a³ +b³ = (a+b)(a² –ab +b²) - сума кубів

a³ –b³ = (a –b)(a² +ab +b²) – різниця кубів

Відмітимо, що всі ці формули – тотожності: вони правильні для будь-яких значень.

Кожну з цих тотожностей можна використати подвійно, оскільки ліву частину ми можемо звести до правої, а праву до лівої.

Наприклад: Різниця квадратів двох виразів дорівнює добутку різниці цих виразів на суму цих виразів.

а ²- b ² = (а + b)(а – b).

І навпаки добуток різниці двох виразів на суму цих виразів дорівнює різниці квадратів цих виразів:

(а + b)(а – b) = а ²- b ²