Ідея прийому доведень із застосуванням властивостей квадратного тричлена, полягає в наступному. Нехай у випадку, коли у нерівності наявний квадратний тричлен відносно деякої змінної, встановлено, що він не має коренів. Тоді при умові додатності старшого коефіцієнта потрібно, щоб дискримінант цього тричлена був від’ємним.
Навпаки, якщо нам вдається показати, що корені є, то цим самим ми фактично обґрунтовуємо, що дискримінант квадратного тричлена не може бути від’ємним. Іноді питання наявності коренів може виявитися дещо складнішим і тоді можна пробувати з’ясовувати, чи існують значення змінних, при яких вираз приймає значення різних знаків. Цього у випадку неперервності функції було б достатньо, щоб стверджувати факт наявності коренів.
Наведемо приклади задач.
Задача2.2.1. Якщо 
, то 
. Довести.
Доведення. Якщо 
, то нерівність очевидна. Нехай 
. Зведемо нерівність до виду 
та розглянемо квадратне рівняння 
. Очевидно, що рівняння має корені (зокрема коренем є значення 
). Тому дискримінант 
рівняння задовольняє умову 
, звідки отримуємо потрібну нерівність . Рівність можлива при рівних значеннях всіх змінних.
Задача2.2.2. Для невід’ємних чисел 
довести нерівність 
.
Доведення. Нехай 
. Запишемо нерівність у виді
та розглянемо квадратне рівняння 
. Очевидно, що рівняння має корені (зокрема коренем рівняння є значення ). Тому дискримінант рівняння задовольняє умову 
. Звідси отримуємо потрібну нерівність. Рівність можлива при рівних значеннях всіх змінних.
Задача 2.2.3. Довести, що при всіх 
виконується нерівність
.
Розв’язання. Розглянемо квадратний тричлен
.
Знайдемо його значення в точках 
та 
. Маємо:
,
.
Тепер, оскільки при 
,
то можна стверджувати, що в точках та функція приймає значення різні за знаком. Тому на відповідному проміжку існує корінь квадратного тричлена. Отже, його дискримінант 
додатний, а це доводить задану нерівність.
При 
нерівність набуває виду 
або 
. Записавши її у виді 
, бачимо, що при 
вона вірна.
Задача 2.2.4. Довести, що для всіх дійсних значень 
виконується нерівність 
.
Розв’язання. Різницю 
можна вважати дискримінантом квадратного тричлена 
. Даний тричлен має корені 
та 
, тому його дискримінант не може бути від’ємним. Знак рівності можливий, коли ці корені рівні, тобто при 
або 
.
Задача 2.2.5. Відомо, що один із коренів рівняння 
більший 2. Довести, що 
.
Доведення. Нехай 
- корінь, про який іде мова в умові, тобто 
. Маємо 
, 
. Звідси 
або .
Задача 2.2.6. Числа 
такі, що 
. Довести, що 
.
Доведення. При отримуємо нерівність 
, яка не виконується тільки у випадку, коли 
. Але тоді відповідно до умови матимемо 
, що неможливо. Отже, 
і нерівність при виконується.
Нехай 
. Розглянемо функцію 
. Оскільки 
і 
, то відповідно до умови отримуємо 
. Це означає, що на інтервалі 
знаходиться один із коренів квадратного тричлена, тому його дискримінант 
.
Задача 2.2.7. Додатні числа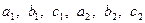 
такі, що 
, 
. Довести, що 
.
Доведення. Короткий аналіз структури нерівності, яку потрібно довести, показує, що вираз
можна розглядати, як дискримінант квадратного тричлена
.
Якщо ми зуміємо показати, що цей тричлен приймає тільки додатні значення, то цим самим доведемо, що 
. Відповідно до умови квадратні тричлени 
та 
такі, що при довільному 
виконуються нерівності 
, 
. Очевидна також нерівність 
. Додавши три одержані співвідношення, отримаємо нерівність, яку доводимо.
Задача 2.2.8. При яких значеннях параметра сума квадратів коренів рівняння 
буде найменшою?
Розв’язання. Нехай 
та 
- корені заданого рівняння. За теоремою Вієта маємо 
. Тому
.
Найменше значення одержаного виразу дорівнює 1 і досягається воно при . Залишається зауважити, що при дійсні корені рівняння існують. Без цієї перевірки вважати розв’язання задачі завершеним не можна. Наприклад, для аналогічної задачі з рівнянням 
подібні міркування у вигляді перетворень
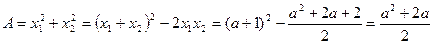
привели б до неправильної відповіді 
. При цьому значенні рівняння дійсних коренів не має.
Задача 2.2.9. Довести, що для будь-яких дійсних чисел та 
виконується нерівність 
.
Доведення. Перетворимо заданий вираз наступним чином:
.
Очевидно, що одержаний вираз не може бути від’ємним, а значення 0 досягається при виконанні умов 
, тобто при 
.
Даний результат можна було отримати і за допомогою інших міркувань, зокрема досліджуючи дискримінант лівої частини нерівності, розглядаючи її, як квадратну відносно змінної або .
Задача 2.2.10. Довести нерівність 
.
Доведення. Зробимо наступні перетворення:
.
Отриманий вираз не може бути від’ємним, а це доводить вказане в умові твердження. Рівність можлива при . Цей самий результат випливає з того, що дискримінант квадратного тричлена 
відносно змінної , який дорівнює 
, не може бути додатним.
Задача 2.2.11. Довести нерівність 
(приклад 1.2.6).
Доведення. Дискримінант квадратного тричлена 
відносно змінної , який дорівнює 
, не може бути додатним. Це означає, що даний вираз не може приймати від’ємні значення. Знак рівності досягається при 
.
Задача 2.2.12. Довести, що при довільному дійсному виконується нерівність
.
Доведення. Перетворимо нерівність до виду
та розглянемо її ліву частину, як квадратний тричлен відносно 
. Дискримінант цього квадратного тричлена 
. Оскільки 
, то 
. Тому вираз 
не може приймати від’ємні значення, що завершує доведення нерівності. Знак рівності досягається при 
.
Зауважимо, що в результаті нами одночасно отримано розв’язки відповідних тригонометричних рівняння та нерівності.
Застосування похідної
Розглянемо, як при доведені нерівностей можна використовувати похідну. Суть цього прийому полягає в наступному.
Нехай на певному проміжку 
із області визначення функцій 
та 
потрібно довести нерівність 
. Введемо в розгляд функцію 
. Нехай похідна 
має на відрізку, що розглядається, єдиний корінь , це значення є точкою мінімуму функції 
, а також виконується нерівність 
. Тоді цього достатньо, щоб стверджувати, що на проміжку 
виконується нерівність .
Даний прийом можна використовувати і при доведенні числових нерівностей. Для цього спочатку вводять у розгляд деяку функцію, яка приймає задані числові значення у певних точках, після чого приступають до реалізації описаної вище схеми.
Наведемо приклади таких доведень.
Задача 2.3.1. Довести нерівність
.
Доведення. ОДЗ: 
. Очевидно, що при 
ми отримуємо рівність. Розглянемо функцію 
. Її похідна 
дорівнює 0 в точці і монотонно зростає (останнє випливає з того, що її похідна 
додатна). Таким чином, для функції 
точка є точкою екстремуму, а саме точкою мінімуму. Тому для всіх , що належать ОДЗ, виконується нерівність 
, що і потрібно було довести.
Зауважимо, що одночасно нами фактично розв’язане рівняння 
з єдиним коренем 
та нерівність 
з розв’язками 
.
Задача 2.3.2. При 
виконується нерівність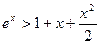 
. Довести.
Доведення. Розглянемо функцію 
. Знайшовши 
та 
, бачимо, що друга похідна перетворюється в 0 у точці і при переході через цю точку змінює знак із «-» на «+». Це означає, що для функції 
точка є точкою мінімуму і 
. Таким чином, 
на всій числовій осі. Звідси випливає, що функція 
монотонно зростає. Оскільки 
, то при 
маємо 
. Нерівність доведена.
Одночасно нами отримано наступні результати:
рівняння 
має єдиний корінь ;
нерівність 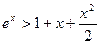має розв’язки 
.
розв’язками нерівності 
є проміжок 
.
Задача 2.3.3. Довести, що при 
для всіх натуральних 
виконується нерівність 
(нерівність Бернуллі).
Доведення. При 
нерівність вірна. Нехай 
. Розглянемо функцію 
. Її похідна 
перетворюється в нуль у єдиній точці , яка, як легко бачити,, є точкою мінімуму. Тому для всіх виконується нерівність 
, тобто 
. З одержаного співвідношення випливає нерівність Бернуллі.
Задача 2.3.4. Довести, що при 
виконується нерівність
.
Доведення. Розглянемо тільки випадок 
, оскільки при 
перепозначення змінних на 
та 
на 
приведе нас до аналогічних міркувань. При маємо очевидну рівність. Нехай 
. Введемо заміну 
та розглянемо функцію 
. Очевидно, що похідна 
не перетворюється в нуль у жодній точці і, оскільки 
та 
, то , монотонно зростаючи, не може приймати від’ємних значень. Тому 
, що доводить задану нерівність.
Задача 2.3.5. Довести нерівність (приклад 2.2.10).
Доведення. Нехай . Розглянемо функцію 
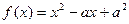. Її похідна 
перетворюється в нуль у точці 
. Очевидно, що це є точка мінімуму і 
. Оскільки 
, то 
, що фактично і потрібно було довести. Рівність виконується при .
Задача 2.3.6. Довести, що для всіх дійсних виконується нерівність 
.
Доведення. Розглянемо функцію 
. Маємо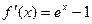 
. Рівність похідної нулю досягається при . Очевидно, що знайдене значення є точкою мінімуму. Для значень 
буде виконуватися нерівність 
. Рівність виконується при .
Задача 2.3.7. Довести, що для всіх дійсних виконується нерівність
.
Доведення. Розглянемо функцію 
. Похідна 
приймає значення 0 в єдиній точці . Очевидно, що це значення є точкою мінімуму. Тому для значень буде виконуватися нерівність 
. Рівність досягається при .
Задача 2.3.8. Довести, що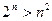 
для всіх натуральних 
.
Доведення. Розглянемо функцію 
та знайдемо її похідну. Маємо 
. Оскільки
,
то на проміжках 
, 
похідна має принаймні по одному кореню. Більше коренів рівняння 
мати не може. Справді, рівняння 
має єдиний корінь (оскільки 
і 
для достатньо великих ). Тому функція 
має єдину точку екстремуму – а саме точку мінімуму, а рівняння у нашому випадку має тільки два корені. Таким чином обґрунтовано, що похідна на проміжку 
приймає додатні значення і функція зростає. Отже, 
. Нерівність 
на проміжку 
виконується для довільних , тому і для всіх натуральних , вибраних у цій множині.
Зауважимо, що інше доведення цієї нерівності методом математичної індукції наведене нами у виді задачі 1.6.3.
Задача 2.3.9. Довести нерівність 
.
Доведення. Зробимо наступні перетворення:
.
Перший множник отриманого виразу приймає тільки додатні значення. Покажемо, що і другий множник теж завжди додатний. Для цього розглянемо функцію 
. Її похідна 
перетворюється в нуль в точках та 
. Легко переконатися, що при екстремуму нема, а точка є точкою мінімуму. Оскільки 
, то функція приймає тільки додатні значення.
Задача 2.3.10. Порівняти числа 
та 
.
Розв’язання. Порівняємо натуральні логарифми цих чисел, тобто числа 
та 
, що рівносильне поставленій задачі, оскільки функція 
монотонно зростає на своїй області визначення. Для цього розглянемо функцію 
, визначену на інтервалі 
. Встановимо проміжки її монотонності. Очевидно, що похідна 
перетворюється в нуль у точці 
. Легко встановити, що це точка максимуму і що на проміжку 
функція монотонно спадає. Оскільки цьому проміжку належать числа 
та 
, то більшому з них відповідає менше значення функції. Тому 
і 
.
Задача 2.3.11. Довести, що при 
виконується нерівність 
.
Доведення. Доведемо нерівність 
, яка на вказаному проміжку рівносильна заданій. Розглянемо функцію 
на інтервалі 
та доведемо, що на ньому вона зростає. Для цього достатньо показати, що 
. Маємо
.
Оскільки знаменник похідної на вказаному проміжку додатний, то покажемо, що додатним є також чисельник, тобто, що виконується нерівність 
. А це випливає з нерівності 
для 
та 
при 
. Отже, і функція зростає на інтервалі . Тому для або .
Застосування інтеграла.
Використання інтегрального числення при доведенні нерівностей використовує наступні міркування. Нехай на проміжку задані дві неперервні функції 
та 
і в усіх точках цього проміжку виконується нерівність 
. Тоді на заданому відрізку виконується також нерівність 
. Аналогічне твердження стосується також випадків 
, 
та 
.
Алгоритм використання даного прийому може виглядати наступним чином. Для доведення нерівності 
розглядаємо функції та , де 
, 
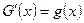. Якщо виконується нерівність , то стверджуємо, що вірна нерівність 
.
Задача 2.4.1. Довести, що при 
виконуються нерівності
, 
.
Розв’язання. Оскільки на вказаному проміжку виконується нерівність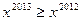 
, то 
. Звідси знаходимо . Інтегруючи одержану нерівність ще раз, маємо
.
З одержаної нерівності отримуємо, що .
Задача 2.4.2. Довести нерівність
.
Розв’язання. Розглянемо функцію 
, значення якої наявні в нерівності. Оскільки кожний доданок 
можна трактувати, як площу прямокутника з висотою та основою, що дорівнює 1 (відстань між точками та 
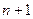), то
.
