Нерівність Єнсена
Розглянемо функцію  , визначену та диференційовану на відрізку
, визначену та диференційовану на відрізку  і позначимо через
і позначимо через  частину її графіка, що відповідає відрізку
частину її графіка, що відповідає відрізку  .
.
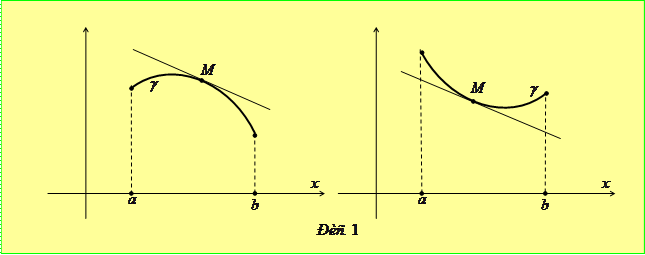 Функцію
Функцію  називають опуклою вгору (вниз) на відрізку
називають опуклою вгору (вниз) на відрізку  , якщо для довільної точки
, якщо для довільної точки  крива
крива  лежить нижче (вище) від дотичної до
лежить нижче (вище) від дотичної до  , проведеної в точці
, проведеної в точці  (рис. 1).
(рис. 1).
Серед деяких властивостей опуклих функцій відмітимо ті, які в подальшому використаємо при доведенні деяких нерівностей.
1. Якщо функція  на відрізку
на відрізку  опукла вгору, то для двох довільних різних точок
опукла вгору, то для двох довільних різних точок  виконується нерівність
виконується нерівність
 .
.
2. Якщо функція  на відрізку
на відрізку  опукла вниз, то для двох довільних різних точок
опукла вниз, то для двох довільних різних точок  виконується нерівність
виконується нерівність
 .
.
 Доведення обох тверджень очевидне. Зокрема у першому випадку достатньо побачити, що довжина відрізка
Доведення обох тверджень очевидне. Зокрема у першому випадку достатньо побачити, що довжина відрізка  , який дорівнює
, який дорівнює  , менша від довжини відрізка
, менша від довжини відрізка  , який дорівнює
, який дорівнює  (рис. 2).
(рис. 2).
3. Якщо функція  на відрізку
на відрізку  опукла вгору і числа
опукла вгору і числа  не всі рівні між собою, то виконується нерівність
не всі рівні між собою, то виконується нерівність
 . (*)
. (*)
4. Якщо функція  на відрізку
на відрізку  опукла вниз і числа
опукла вниз і числа  не всі рівні між собою, то виконується нерівність
не всі рівні між собою, то виконується нерівність
 . (**)
. (**)
Доведення двох останніх тверджень можна реалізувати за допомогою методу математичної індукції.
Нерівності (*), (**), які у математиці називають нерівностями Єнсена, можуть служити основою для складання та доведення різних нерівностей. Достатньо вибрати конкретну функцію, опуклу вгору або вниз та замінити нею функцію  .
.
Наведемо приклади подібних доведень.
Задача 2.5.1. Довести, що для різних  виконується нерівність
виконується нерівність
 .
.
Доведення. Для доведення достатньо у співвідношенні (*) використати замість  функцію
функцію  , графік якої на вказаному відрізку опуклий вверх.
, графік якої на вказаному відрізку опуклий вверх.
Задача 2.5.2. Довести, що для довільних чисел  виконується нерівність
виконується нерівність
 .
.
Доведення. Тут ми повертаємося до розгляду задачі 1.3.2. У цьому випадку використовуємо співвідношення (**), а в ролі  функцію
функцію  , графік якої при
, графік якої при  опуклий вниз.
опуклий вниз.
Задача 2.5.3. Порівняти числа  та
та  .
.
Доведення. Розглянемо функцію  , графік якої на проміжку
, графік якої на проміжку  опуклий вниз. Застосувавши нерівність Єнсена у виді співвідношення (**), отримуємо
опуклий вниз. Застосувавши нерівність Єнсена у виді співвідношення (**), отримуємо
 .
.
Тому

 .
.
Задача 2.5.4. Довести, що правильний  -кутник має найбільший периметр серед усіх вписаних в коло
-кутник має найбільший периметр серед усіх вписаних в коло  -кутників.
-кутників.
Доведення. Нехай  -кутник
-кутник  вписаний у коло з центром у точці
вписаний у коло з центром у точці  та радіусом
та радіусом  . Позначимо
. Позначимо  . Тоді
. Тоді  (знак строгої нерівності буде у випадку, коли центр кола лежить поза многокутником). Користуючись теоремою косинусів отримуємо, що для периметра многокутника
(знак строгої нерівності буде у випадку, коли центр кола лежить поза многокутником). Користуючись теоремою косинусів отримуємо, що для периметра многокутника  маємо
маємо
 .
.
Оскільки  і функція
і функція  на вказаній множині значень опукла вгору, то з нерівності Єнсена отримуємо, що
на вказаній множині значень опукла вгору, то з нерівності Єнсена отримуємо, що
 ,
,
а саме останньому значенню дорівнює периметр правильного вписаного в коло многокутника.
Розглянемо, як нерівність Єнсена та наведені міркування можна використати для доведення класичних нерівностей між середніми. Як ми уже знаємо (розділ 1.7), для  додатних чисел
додатних чисел 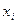 такими є середнє арифметичне
такими є середнє арифметичне  , середнє геометричне
, середнє геометричне  , середнє квадратичне
, середнє квадратичне  та середнє гармонічне
та середнє гармонічне 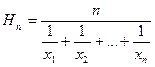 . Ці середні величини знаходяться у співвідношеннях
. Ці середні величини знаходяться у співвідношеннях 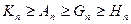 . Знак рівності в усіх випадках виконується тоді і тільки тоді, коли
. Знак рівності в усіх випадках виконується тоді і тільки тоді, коли 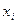 рівні. Доведемо строгі нерівності, вважаючи
рівні. Доведемо строгі нерівності, вважаючи 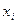 різними.
різними.
Для доведення першої нерівності  , тобто
, тобто
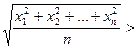

використаємо у ролі  функцію
функцію  , графік якої опуклий вниз, та співвідношення (**). Відповідно до нього отримуємо
, графік якої опуклий вниз, та співвідношення (**). Відповідно до нього отримуємо
 ,
,
звідки, добувши корінь з обох частин, дістаємо шукане співвідношення.
Для доведення другої нерівності  , тобто
, тобто


використаємо у ролі  функцію
функцію 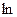 , графік якої опуклий вгору, та співвідношення (*). Отримуємо
, графік якої опуклий вгору, та співвідношення (*). Отримуємо

або
 .
.
Потенціюючи одержаний вираз, отримуємо шукане співвідношення.
Для доведення останньої нерівності  , тобто нерівності між середнім геометричним та середнім гармонічним
, тобто нерівності між середнім геометричним та середнім гармонічним

 ,
,
знову використаємо функцію 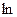 , тільки співвідношення (*) застосуємо до чисел
, тільки співвідношення (*) застосуємо до чисел  . Отримуємо
. Отримуємо

або

 ,
,
що фактично завершує доведення потрібної нерівності.
Нерівність Юнга
 Нехай
Нехай  – неперервна строго зростаюча функція від
– неперервна строго зростаюча функція від 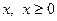 , і
, і  (див. рис. 3). Розглядаючи площі, представлені відповідними інтегралами, ми переконуємося в тому, що
(див. рис. 3). Розглядаючи площі, представлені відповідними інтегралами, ми переконуємося в тому, що
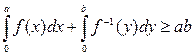 , (***)
, (***)
де 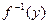 - функція, обернена до
- функція, обернена до  . Легко бачити, що рівність тут має місце тільки при
. Легко бачити, що рівність тут має місце тільки при  . Ця нерівність називається нерівністю Юнга. Вибираючи у ролі
. Ця нерівність називається нерівністю Юнга. Вибираючи у ролі  різні функції, ми отримуємо ряд цікавих результатів.
різні функції, ми отримуємо ряд цікавих результатів.
Візьмемо, наприклад, у ролі функції  функцію
функцію  , p >1, оберненою до якої є функція
, p >1, оберненою до якої є функція  . У цьому випадку співвідношення (***) приймає вид
. У цьому випадку співвідношення (***) приймає вид
 ,
,
де  .
.
Нехай  і
і  . Тоді отримуємо, що при
. Тоді отримуємо, що при  виконується нерівність
виконується нерівність  .
.
Вибираючи в ролі функції  функцію
функцію  та використовуючи обернену до неї функцію
та використовуючи обернену до неї функцію  із (***) знаходимо
із (***) знаходимо
 .
.
Замінюючи  на
на  , отримуємо нерівність
, отримуємо нерівність  . Одержане співвідношення в математиці застосовується в теорії рядів Фур’є.
. Одержане співвідношення в математиці застосовується в теорії рядів Фур’є.
Нехай  . Тоді
. Тоді  . Користуючись нерівністю Юнга, знаходимо
. Користуючись нерівністю Юнга, знаходимо
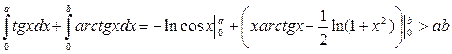 ,
,
звідки отримуємо нерівність
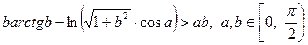 .
.
При  дістаємо
дістаємо  або
або  .
.
Таким чином, доведена нерівність  .
.






