Нехай нам потрібно довести нерівність 
, де 
- де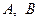які числові вирази або вирази із змінними. Вважатимемо, що є очевидною, або легко доводиться нерівність 
. Якщо нам вдасться довести нерівності 
та 
, то, очевидно, що задача буде розв’язаною. Це випливає з ланцюжка нерівностей 
. Іноді такий ланцюжок може бути довшим, а іноді навіть коротшим, якщо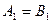 
. Наприклад, щоб довести числову нерівність 
, достатньо зауважити, що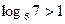 
, а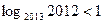 
. Такий прийом у доведеннях нерівностей називають методом підсилення.
При застосуванні цього методу часто використовують співвідношення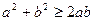 
, 
при 
, 
при 
, 
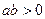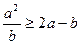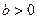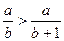при 
, 
при 
.
Наведемо приклади подібних доведень.
Задача 1.5.1. Довести нерівність
.
Доведення. Маємо
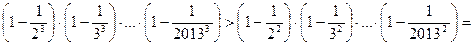
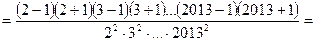
Задача 1.5.2. Довести, що при 
виконується нерівність
.
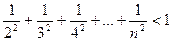Доведення. Маємо
, 
,…, 
.
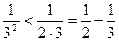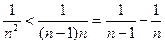Додаючи дані нерівності, дістаємо
.
Отже, .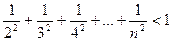
Задача 1.5.3. Довести нерівність
.
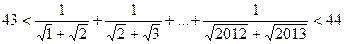Доведення. Позбудемося ірраціональності у знаменниках дробів. Оскільки
,
то
.
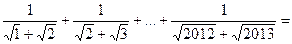
Для доведення нерівності залишається зауважити, що
.
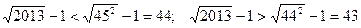Задача 1.5.4. Довести нерівність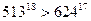 
.
Розв’язання.
.
Задача 1.5.5. Довести нерівність
,
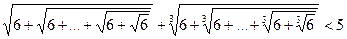якщо у кожному з доданків використано 2013 радикалів.
Доведення.
.
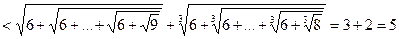Задача 1.5.6. Для додатних чисел 
довести нерівність 
.
Доведення. Використовуючи двічі нерівність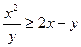 
, де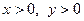 
, отримуємо
,
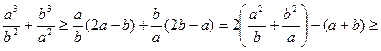
що і потрібно було довести.
Задача 1.5.7. Довести нерівність 
.
Доведення. Очевидні нерівності
, 
, …,
, 
.
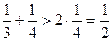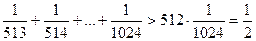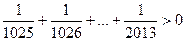Додавши їх та перший доданок суми, тобто число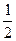 
, дістаємо потрібну нерівність.
Задача 1.5.8. Порівняти числа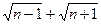 
та 
при 
.
Розв’язання. Порівняємо квадрати цих додатних чисел, тобто вирази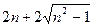 
та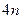 
або числа 
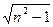та 
. Очевидно, що 
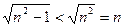, тому перше із заданих чисел менше.
Задача 1.5.9. Довести, що 
.
Доведення. Очевидно, що 
, 
, 
,…, 
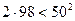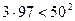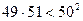. Перемноживши ці нерівності, отримаємо, що .
Задача 1.5.10. Довести, що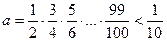 
.
Доведення. Очевидно, що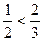 
, 
, …, 
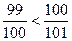. Тому
.
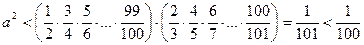Отже,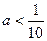 
.
Задача 1.5.11. Довести, що для всіх додатних чисел 
, для яких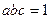 
, виконується нерівність
.
Доведення. При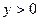 
із очевидної нерівності 
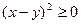випливає, що 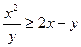. Використаємо одержане співвідношення для перетворення доданків заданої нерівності. Дістаємо:
.
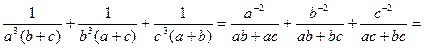
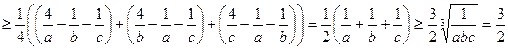При виконанні перетворень для чисел 
у кінці доведення використано нерівність між середнім арифметичним та середнім геометричним, які ми більш детально розглянемо в пункті 1.7. Рівність у заданому співвідношенні досягається тільки при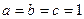 
.
Задача 1.5.12. Довести, що для довільних додатних чисел 
виконується нерівність 
.
Доведення. Використовуючи нерівність 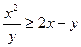, отримуємо
.
Зауважимо, що нерівності, одну з яких ми доводимо, та друга, яку використовуємо при доведенні, є частинним випадком нерівності 
, яка випливає з тотожності
.
Задача 1.5.13. Для чисел 
, кожне з яких не менше 1, довести нерівність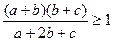 
.
Доведення. Відповідно до умови маємо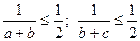 
.Тому
.
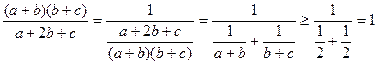Рівність досягається тільки при .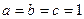
Задача 1.5.14. Для чисел , кожне з яких не менше 2, довести нерівність 
.
Доведення. Очевидно, що при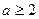 
виконується нерівність 
. Аналогічно при 
маємо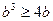 
і при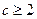 
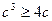. Тому
.
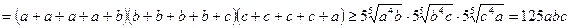Рівність досягається при 
.
Задача 1.5.15. Довести, що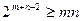 
для всіх натуральних чисел 
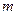та .
Доведення. Очевидно, що задача зводиться до доведення нерівності 
, оскільки після підстановки в неї значень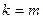 
та 
і перемноження одержаних нерівностей отримуємо співвідношення, що доводиться. Тепер маємо, що при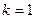 
виконується знак рівності, а при 
, використовуючи біном Ньютона, дістаємо
.
Задача 1.5.16. Знайти найбільше та найменше значення виразу 
, якщо числа належать відрізку 
.
Доведення. Виконаємо наступні перетворення:
.
Згідно з умовою задачі маємо
.
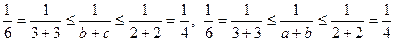Таким чином, величина знаменника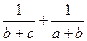 
змінюється у межах від 
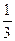до 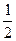, а величина заданого виразу – від 2 до 3. Найбільше та найменше значення досягаються при та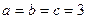 
.
Задача 1.5.17. Сума двох додатних чисел дорівнює 2013. Довести, що ці числа задовольняють нерівність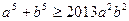 
.
Доведення. Запишемо задане в умові співвідношення у виді 
та, використовуючи двічі нерівність 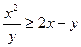, перетворимо його ліву частину. Отримуємо
,
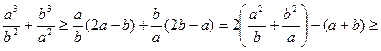
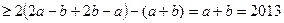що і потрібно було довести.
Задача 1.5.18. Довести, що для всіх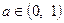 
виконується нерівність
.
Доведення. Запишемо нерівність у виді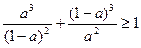 
. Тепер, міркуючи, як і у попередній задачі, отримуємо
,
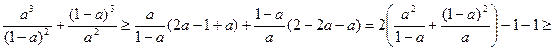
що і потрібно було довести.
Задача 1.5.19. Якщо 
- натуральні числа, то 
. Довести.
Доведення. Доведення випливає із співвідношення 
, оскільки кожен з трьох доданків у лівій частині не перевищує 1. Рівність можлива тільки у випадку 
.
