Повернемося до нерівності 
, де 
. Як було зауважено вище, знак рівності тут виконується тоді і тільки тоді, коли всі значення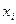 
рівні. Звідси можна отримати два цікавих факти, які мають ряд застосувань.
1. Якщо добуток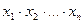 
є сталою величиною, то сума 
приймає найменше значення. При 
це значення дорівнює 
.
2. Якщо сума є сталою величиною, то добуток 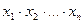приймає найбільше значення. При 
воно дорівнює 
.
Наведені міркування дозволяють доводити окремі нерівності з новими постановками задач.
Задача 1.8.1. Знайти найбільше і найменше значення функції
.
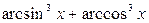Розв’язання. Нехай 
, 
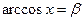. Оскільки 
, то
.
Значення функції буде найменшим, коли найбільшим буде значення добутку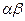 
.
Оскільки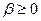 
, то найбільше значення 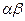потрібно шукати при 
. Із нерівності Коші маємо 
. Але 
, тому 
. Найбільше значення 
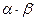прийматиме при 
. Тоді: 
і найменше значення функції буде 
.
Найменше значення 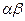очевидно буде при 
. При 
маємо 
, 
. Враховуючи ці значення, бачимо, що добуток буде мінімальним, оскільки 
приймає мінімальне значення, а 
- максимальне. Отже, при функція приймає найбільше значення
.
Таким чином, найбільшим значенням буде 
а найменшим 
.
Задача 1.8.3. Знайти найбільше значення виразу 
, якщо 
.
Розв’язання. Згідно з умовою вираз 
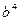(а, отже, і 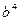) прийматиме найбільше значення при = 
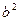, тобто при 
. При цьому 
.
Задача 1.8.4. Знайти найменше значення виразу 
, якщо 
.
Розв’язання. Оскільки добуток виразів та 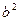є сталим (із умови випливає, що 
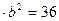), то вираз прийматиме найменше значення при = 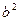, тобто при 
. При цьому 
, звідки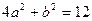 
.
Задача 1.8.5. Знайти найбільше значення функції 
.
Розв’язання. При 
значення функції дорівнює 0. При 
запишемо вираз для функції у виді 
. Дослідимо, коли знаменник виразу найменший. Зауваживши, що добуток виразів 
та 
є сталим числом, робимо висновок, що знаменник найменший при 
, тобто при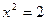 
. Значення функції при цьому є максимальним і буде дорівнювати 
.
Задача 1.8.6. Довести, що для довільних чисел 
виконується нерівність
.
Доведення. Ми уже розглядали доведення даної нерівності, використовуючи нерівність Коші. Зупинимося на інших міркуваннях. Оскільки добуток чисел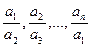 
є сталою величиною, то їхня сума буде
.
Задача 1.8.7. Оцінити значення виразу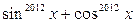 
.
Розв’язання. Нехай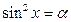 
, 
. Тоді
і сума прийматиме найменше значення, коли добуток 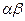найбільший. Оскільки вираз 
є сталим, то максимальне значення буде при 
, тобто, коли 
або при 
. Значення заданого виразу у цьому випадку дорівнює 
. Одержали нижню оцінку виразу. Верхня оцінка випливає з нерівностей 
. Рівність досягається у точках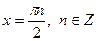 
.
Таким чином, 
.
Розділ 2. Застосування властивостей функцій при доведенні нерівностей
