1. Знайти положення рівноваги прямокутної мембрани 0≤ x ≤π, 0≤ y ≤ a, край x =0 якої нерухомо закріплений, на краях x =π та y =0 діють сили відповідно 
та 
а край y = a пружно закріплений (h =1), причому край закріплення пружини зміщується за законом 
.
2. Знайти стаціонарний розподіл температури у прямокутній пластинці 0≤ x ≤1, 0≤ y ≤2π, на краї y =2π якої підтримується стала температура 
, краї x =1 та y =0 теплоізольовані, а на краї x =0 проходить теплообмін (із коефіцієнтом h =1) із навколишнім середовищем, температура якого рівна 
.
3. Визначити форму прогину прямокутної мембрани 0≤ x ≤ a, 0≤ y ≤ b під дією зовнішньої сили 18 xy, якщо краї x =0 та x = a мембрани нерухомо закріплені, а інші вільні.
4. Визначити стаціонарний розподіл температури у прямокутній пластинці 0≤ x ≤ a, 0≤ y ≤ b, два краї y =0 та x = a якої підтримуються при нульовій температурі, а інші теплоізольовані. Усередині пластинки діє джерело тепла інтенсивності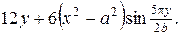 
5. До краю кругової пластинки одиничного радіуса підводиться тепловий потік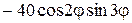 
. Знайти стаціонарний розподіл температури зовні пластинки.
6. Усередині нескінченого кругового циліндра радіуса R проходить рух нестискуваної рідини. Вважаючи рух сталим, потенціальним і плоскопаралельним, знайти закон цього руху, якщо проекція швидкості 
на зовнішню нормаль циліндра у кожній точці задається формулою:
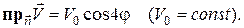
Зауваження. Якщо в області G, обмеженій замкнутою поверхнею S, проходить стаціонарний потенціальний рух нестискуваної однорідної рідини, то для визначення закону цього руху достатньо знайти потенціал U (x,y,z) поля швидкостей , який є розв’язком задачі:
де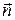 
– зовнішня нормаль до поверхні S, а f (x,y,z) – задана на S функція, рівна проекції швидкості в точках цієї поверхні на зовнішню нормаль. Якщо потенціал U (x,y,z) знайдений, то поле швидкостей 
- 72 -
Якщо область G обмежена циліндричною поверхнею з твірною, паралельною до осі O z, а вектор швидкості не залежить від z, тоді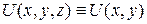 
і є розв’язком задачі:
Тому наведена вище задача зводиться до наступної задачі Неймана:
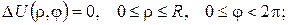
7. Знайти форму прогину мембрани, яка має вигляд кільця 1≤ρ≤2, 0≤φ<2π, якщо:
а) на внутрішній край мембрани діє сила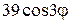 
, а на зовнішньому задане відхилення 
;
б) на внутрішньому краї мембрани задане відхилення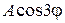 
, а на зовнішній діє сила 
(A = const).
8. Усередині круглоїпластинки радіуса a діють джерела тепла інтенсивності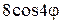 
, а її край підтримується при нульовій температурі. Знайти стаціонарний розподіл температури в пластинці.
9. Визначити прогин мембрани, яка має форму кільця 1≤ρ≤2, 0≤φ<2π, якщо:
а) мембрана піддається дії сили 
, на внутрішньому краї відхилення рівне 
, а зовнішній край вільний;
б) мембрана піддається дії сили 
, внутрішній край нерухомо за-кріплений, а на зовнішньому краї задана стала сила A = const.
10. Проінтеґрувати крайові задачі та дати фізичну інтерпретацію:
а) 
б)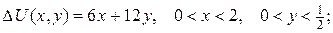 
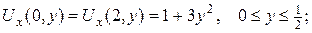
в)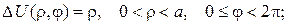 
г) 
ґ) 
- 73 -
д) 
е)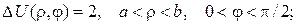 
є) 
11. Побудувати функцію Ґріна задачі Діріхле:
а) в крузі 0≤ρ≤ R, 0≤φ<2π;
б) у круговому секторі 0≤ρ≤ R, 0≤φ≤π/n; nÎ N.
12. Знайти об’ємний потенціал 
кулі радіуса R з центром у початку координат при сталій густині заряду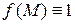 
:
а) поставивши крайову задачу для і розв’язавши її;
б) шляхом прямого обчислення об’ємного інтеґралу.
13. Знайти потенціал простого шару, розподілений зі сталою густиною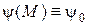 
на сфері одиничного радіуса з центром у початку координат.
14. Знайти лоґарифмічний потенціал подвійного шару відрізка 0£ х £ а зі сталою густиною моментів 
15. За допомогою потенціалу подвійного шару розв’язати задачу Діріхле для півплощини:
Розглянути випадок 
16. Користуючись потенціалом простого шару, знайти розв’язок задачі Неймана для круга одиничного радіуса з центром у початку координат:
- 74 -
ВІДПОВІДІ
1. 
2. 
3. 
4. 
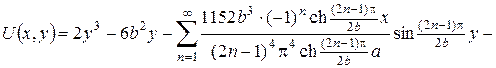
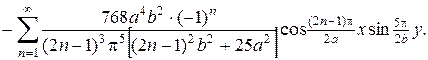
5. 
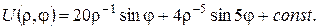
6. 
7. а)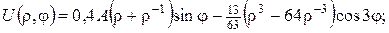 
б) 
8. 
9. а) 
б) 
10. а)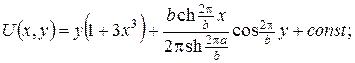 
б) 
в)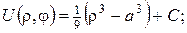 
г) 
ґ) 
- 75 -
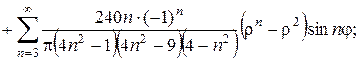
д)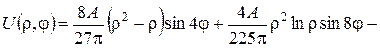 
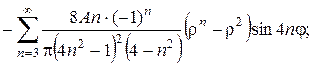
е) 
є) 
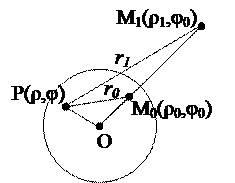11. а) 
причому (див. малюнок)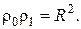 
б)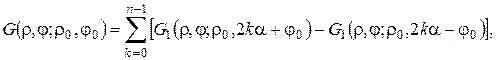 
де 
– розв’язок попередньої задачі,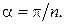 
12. 
13. 
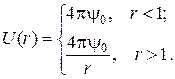
14. 
15. 
при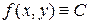 
16. 
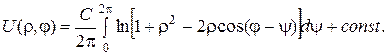
- 76 -
