До рівнянь еліптичного типу приводить вивчення стаціонарних процесів різної фізичної природи (теплопровідність, дифузія, рівновага та інші). Одним із простіших рівнянь еліптичного типу є рівняння Лапласа
Визначення. Функція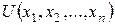 
називається гармонічною в обмеженій області D, якщо вона в цій області двічі неперервно-диференційовна по всіх арґументах і справджує рівняння Лапласа.
Функція 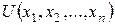називається гармонічною в нескінченій області D*, якщо в кожній точці цієї області, що знаходиться на скінченій віддалі від початку координат, функція двічі неперервно-диференційовна по всіх арґументах, справджує рівняння Лапласа і для досить великих 
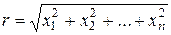має місце нерівність (умова реґулярності на нескінченості)
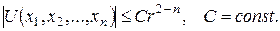
У випадку двовимірного простору умова реґулярності на нескінченості набуває вигляду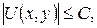 
С=соnst, тобто є умовою обмеженості функції для досить великих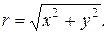 
Рівняння 
називається рівнянням Пуассона.
Теорема 1 (принцип мінімакса для гармонічних функцій). Гармонічна в обмеженій області D і неперервна в замиканні 
функція 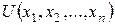досягає свого найбільшого і найменшого значення на границі 
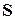області D.
Наведемо постановку основних крайових задач для рівняння Лапласа.
1. Внутрішня (зовнішня) задача Діріхле: знайти гармонічну в D (D*) і неперервну в 
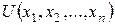( *) функцію , яка на границі 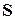області набуває заданих значень: 
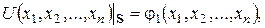де 
– задана неперервна на 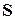функція.
2. Внутрішня (зовнішня) задача Неймана: знайти гармонічну в D (D*) і неперервну разом із частинними похідними першого порядку в ( *) функцію 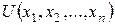, яка на границі 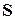області справджує умову
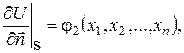
- 44 -
де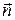 
– зовнішня нормаль до 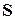, а 
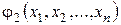– задана неперервна на 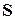функція, яка для коректності постановки задачі повинна справджувати умову
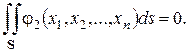
(умова стаціонарності теплового поля).
3. Третя внутрішня (зовнішня) крайова задача: знайти гармонічну в D (D*) і неперервну разом із частинними похідними першого порядку в ( *) функцію 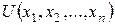, яка на границі 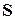області справджує умову
де 
і 
– задані неперервні на 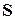функції.
Аналоґічно ставляться крайові задачі і для рівняння Пуассона.
Теорема 2. Як внутрішня, так і зовнішня задачі Діріхле для рівняння Пуассона мають не більш ніж один розв’язок у розглядуваній області (тобто: якщо розв’язок задачі Діріхле існує, то він є єдиним).
Теорема 3. У двовимірному просторі довільні два розв’язки задачі Неймана (внутрішньої чи зовнішньої), які мають неперервні аж до 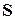частинні похідні першого порядку, відрізняються на сталий доданок.
Зауваження. У випадку трьох і більше незалежних змінних твердження теореми 2 справджується для внутрішньої задачі Неймана. Розв’язок зовнішньої задачі Неймана є єдиним.
Окрім сформульованих трьох основних крайових задач для рівнянь еліптичного типу, на практиці зустрічаються складніші задачі з крайовими умовами різного роду на частинах границі .
