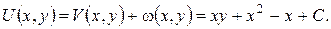Метод власних функцій
А) Метод Фур’є.
Крайові задачі для рівняння Лапласа у випадку прямокутних областей розв’язуються за допомогою методу відокремлення змінних (методу Фур’є) аналоґічно до змішаних задач для рівнянь гіперболічного та параболічного типів.

ПРИКЛАД 1. Знайти розподіл потенціалу  електростатичного поля всередині прямо-кутника ОАСВ зі сторонами ОА=а, ОВ=b (див. малюнок), якщо уздовж сторони ОВ потенціал розподілений згідно закону
електростатичного поля всередині прямо-кутника ОАСВ зі сторонами ОА=а, ОВ=b (див. малюнок), якщо уздовж сторони ОВ потенціал розподілений згідно закону  де
де
- 45 -
 а три інші сторони заземлені. Електричні заряди всередині прямокутника відсутні.
а три інші сторони заземлені. Електричні заряди всередині прямокутника відсутні.
Розв’язання. Складаємо математичну модель задачі:

Шукаючи розв’язок цієї задачі методом відокремлення змінних (крайові умови є узгодженими) у вигляді  з рівняння Лапласа будемо мати
з рівняння Лапласа будемо мати
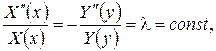
звідки одержимо диференціальне рівняння для функції Х(х)
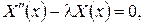
а з урахуванням однорідних крайових умов на сторонах ОА та ВС – задачу Штурма-Ліувілля для функції Y(y):

Розв’язавши останню задачу, одержимо:

(для визначеності можна покласти  ). Підставимо знайдені власні значення
). Підставимо знайдені власні значення  у рівняння для функції Х(х). Загальний розв’язок одержаного рівняння
у рівняння для функції Х(х). Загальний розв’язок одержаного рівняння  запишеться у вигляді
запишеться у вигляді

Тоді

Із крайових умов на сторонах ОВ та АС одержимо систему для визначення невідомих коефіцієнтів  і
і  :
:

де

Отже, для парних п  а для непарних
а для непарних
- 46 -
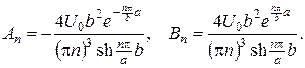
Підставивши ці значення у ряд для розв’язку  і врахувавши непарність п, одержимо
і врахувавши непарність п, одержимо

Зауваження 1. Загальний розв’язок рівняння  часто зручніше записати у вигляді
часто зручніше записати у вигляді

Зауваження 2. У наведеному прикладі ми будували задачу Штурма-Ліувілля для функції  поскільки крайові умови на сторонах
поскільки крайові умови на сторонах  та
та  були однорідними. Якщо ж крайові умови неоднорідні по обох змінних, то таку задачу можна за певних умов звести до двох задач, аналоґічних до прикладу 1. Наприклад, розв’язок крайової задачі
були однорідними. Якщо ж крайові умови неоднорідні по обох змінних, то таку задачу можна за певних умов звести до двох задач, аналоґічних до прикладу 1. Наприклад, розв’язок крайової задачі
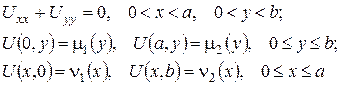
можна шукати у вигляді  де
де  – розв’язок задачі
– розв’язок задачі

а  – розв’язок задачі
– розв’язок задачі

Проте тут слід пам’ятати, що такий спосіб відшукання розв’язку застосовний лише у випадку узгодженості крайових умов не тільки у вихідній, але й у двох дочірніх крайових задачах.
Іноді область, у якій знаходять розв’язок, може бути нескінченою.
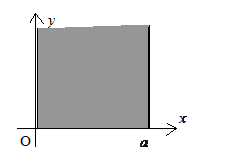
ПРИКЛАД 2. У півсмузі (див. малюнок)  знайти розв’язок
знайти розв’язок  рівняння Лапласа, який справджує наступні крайові умови:
рівняння Лапласа, який справджує наступні крайові умови:
- 47 -

Розв’язання. Шукаючи розв’язок задачі методом відокремлення змінних (крайові умови є узгодженими) у вигляді  аналоґічно до прикладу 1, одержимо:
аналоґічно до прикладу 1, одержимо:


Задачу Штурма-Ліувілля (ЗШЛ) будуємо для функції Х(х), поскільки цього разу однорідними є крайові умови на сторонах х=0 та х=а. Розв’язавши цю ЗШЛ та при знайдених власних значеннях – рівняння для функції Y(y), одержимо:

Враховуючи умову обмеженості розв’язку при  беремо
беремо 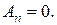 Тоді
Тоді

Для визначення коефіцієнтів  використаємо крайову умову при у=0:
використаємо крайову умову при у=0:
 звідки
звідки 
Отже, розв’язок крайової задачі буде 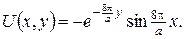
Б) Метод власних функцій.
Розглянемо задачу: в області  знайти розв’язок рівняння Пуассона
знайти розв’язок рівняння Пуассона
 (1)
(1)
який справджує крайові умови
 (2)
(2)
 (3)
(3)
Розв’язок цієї задачі у випадку, коли функція  сама справджує всі чотири крайові умови, можна знайти за допомогою методу власних функцій. Для цього спочатку розв’язуємо відповідну задачу на власні значення вигляду
сама справджує всі чотири крайові умови, можна знайти за допомогою методу власних функцій. Для цього спочатку розв’язуємо відповідну задачу на власні значення вигляду
- 48 -

Шукаючи власні функції наведеної задачі методом відокремлення змінних у вигляді  одержуємо:
одержуємо:
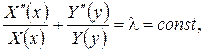
звідки
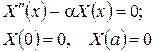




Покладемо для визначеності 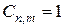 . Тепер розв’язок задачі (1)-(3) можна шукати у вигляді ряду по системі знайдених власних функцій
. Тепер розв’язок задачі (1)-(3) можна шукати у вигляді ряду по системі знайдених власних функцій
 (4)
(4)
Будемо вважати, що ряд (4) рівномірно збігається і його можна почленно диференціювати двічі по х і по у. Для визначення невідомих коефіцієнтів  розкладемо функцію
розкладемо функцію  в подвійний ряд Фур’є по системі власних функцій
в подвійний ряд Фур’є по системі власних функцій 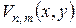 :
:
 (5)
(5)
Підставивши (4) і (5) у рівняння (1), одержимо:

Але

Отже,

Звідси  і згідно (4) розв’язок задачі (1)-(3) буде
і згідно (4) розв’язок задачі (1)-(3) буде

- 49 -
Зауваження. Розв’язок задачі (1)-(3) можна шукати у вигляді ряду (4), поскільки він справджує однорідні крайові умови. У випадку неоднорідних крайових умов, наприклад для задачі
 (6)
(6)
розв’язок при виконанні певних умов (див. попередні приклади) можна шукати у вигляді  де
де  – розв’язок задачі
– розв’язок задачі
 (7)
(7)
а  – розв’язок задачі
– розв’язок задачі
 (8)
(8)
Метод розв’язування задачі (7) поданий у зауваженні 2 до прикладу 1. Задача (8) аналоґічна задачі (1)-(3) й інтеґрується за допомогою методу власних функцій.
Проте не завжди наведені вище методи є раціональними. У деяких частинних випадках можливе застосування більш простих засобів.
ПРИКЛАД 3. Знайти стаціонарний розподіл температури в однорідній прямокутній пластинці 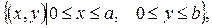 всередині якої діють джерела тепла інтенсивності
всередині якої діють джерела тепла інтенсивності  якщо краї
якщо краї  та
та  пластинки підтримуються при нульовій температурі, а інші два краї теплоізольовані.
пластинки підтримуються при нульовій температурі, а інші два краї теплоізольовані.
Розв’язання. Математична модель задачі:

1 спосіб (метод власних функцій). Вільний член у рівнянні справджує усі чотири крайові умови, тому для відшукання розв’язку застосовний метод власних функцій аналоґічно до задачі (1)-(3). Отже, спочатку розв’язуємо відповідну задачу на власні значення вигляду

Шукаючи власні функції наведеної задачі методом відокремлення змінних у вигляді  легко знаходимо:
легко знаходимо:
- 50 -

Покладемо для визначеності 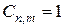 . Тепер розв’язок поставленої задачі можна шукати у вигляді ряду по системі знайдених власних функцій
. Тепер розв’язок поставленої задачі можна шукати у вигляді ряду по системі знайдених власних функцій

Підставивши цей ряд у рівняння, одержимо:
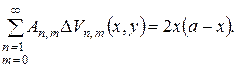
Розкладемо функцію  в подвійний ряд Фур’є по системі знайдених власних функцій
в подвійний ряд Фур’є по системі знайдених власних функцій 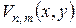 :
:  де
де

Але

Отже,
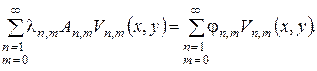
Звідси  і розв’язок задачі матиме вигляд
і розв’язок задачі матиме вигляд
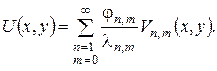
Врахувавши, що коефіцієнти Фур’є  відмінні від нуля тільки при
відмінні від нуля тільки при  і
і 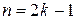 (непарних) і підставивши всі знайдені величини у ряд для
(непарних) і підставивши всі знайдені величини у ряд для 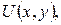 остаточно одержимо:
остаточно одержимо:

Другий спосіб (зведення неоднорідного рівняння до однорідного). Поскільки вільний член у рівнянні є функцією тільки змінної х, а умови на краях  та
та  не залежать від змінної у, то наведену крайову задачу можна розглядати як аналоґ задачі зі стаціонарними неоднорідностями для
не залежать від змінної у, то наведену крайову задачу можна розглядати як аналоґ задачі зі стаціонарними неоднорідностями для
- 51 -
рівнянь гіперболічного та параболічного типів. Отже, шукаємо розв’язок у вигляді
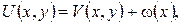
де допоміжна функція  повинна справджувати неоднорідне рівняння та умови на краях
повинна справджувати неоднорідне рівняння та умови на краях  та
та  , тобто повинна бути розв’язком крайової задачі
, тобто повинна бути розв’язком крайової задачі

Проінтеґрувавши цю задачу, одержимо  а для нової невідомої функції
а для нової невідомої функції  – однорідну задачу
– однорідну задачу

звідки очевидно, що  (поскільки рівняння і всі крайові умови є однорідними, а сама задача не є задачею Неймана). Отже, розв’язок вихідної крайової задачі буде
(поскільки рівняння і всі крайові умови є однорідними, а сама задача не є задачею Неймана). Отже, розв’язок вихідної крайової задачі буде
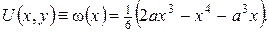
Зауваження. Якщо в задачі для нової невідомої функції  крайові умови неоднорідні, то її розв’язок знаходиться за допомогою методу Фур’є (див. зауваження 2 до прикладу 1). При цьому за вірного підбору допоміжної функції
крайові умови неоднорідні, то її розв’язок знаходиться за допомогою методу Фур’є (див. зауваження 2 до прикладу 1). При цьому за вірного підбору допоміжної функції  або
або  умови застосовності методу Фур’є виконуватимуться автоматично.
умови застосовності методу Фур’є виконуватимуться автоматично.
Завдання. Перевірити тотожність двох одержаних розв’язків крайової задачі для прикладу 3.
ПРИКЛАД 4. Проінтеґрувати задачу та дати фізичну інтерпретацію:

Фізична інтерпретація:
а) знайти положення рівноваги однорідної квадратної мембрани, яка піддається дії зовнішньої сили інтенсивності  якщо край
якщо край  мембрани зміщений на сталу величину, край
мембрани зміщений на сталу величину, край  вільний, до краю
вільний, до краю  прикладена сила
прикладена сила 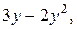 а край
а край  пружно закріплений з коефіцієнтом жорсткості
пружно закріплений з коефіцієнтом жорсткості  причому точки закріплення пружин рухаються за законом
причому точки закріплення пружин рухаються за законом  – або:
– або:
- 52 -
б) знайти стаціонарний розподіл температури в однорідній квадратній пластинці, всередині якої діють джерела тепла інтенсивності  якщо край
якщо край  пластинки підтримується при сталій температурі, край
пластинки підтримується при сталій температурі, край  теплоізольований, до краю
теплоізольований, до краю  підводиться тепловий потік
підводиться тепловий потік 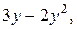 а на краї
а на краї  проходить теплообмін з коефіцієнтом
проходить теплообмін з коефіцієнтом  з навколишнім середовищем, температура якого рівна
з навколишнім середовищем, температура якого рівна 
Розв’язання. Покладемо  де нові невідомі функції є розв’язками наступних крайових задач:
де нові невідомі функції є розв’язками наступних крайових задач:
 (9)
(9)
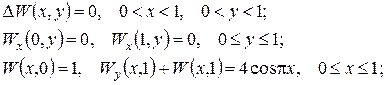 (10)
(10)
 (11)
(11)
Крайові умови в (9) і (10) є узгодженими, тому для відшукання розв’язків цих задач застосовний метод Фур’є.
Отже, 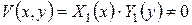 , причому ЗШЛ будуємо для функції
, причому ЗШЛ будуємо для функції  Одержимо:
Одержимо:
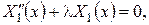

Звідси  де
де  – додатні корені рівняння
– додатні корені рівняння  (ці корені можна визначити лише наближеними методами), а
(ці корені можна визначити лише наближеними методами), а 
 Відповідні функції
Відповідні функції  запишемо для зручності через гіперболічні функції у вигляді
запишемо для зручності через гіперболічні функції у вигляді 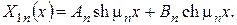 Тоді
Тоді
 (12)
(12)
Коефіцієнти  і
і  визначаємо з умов на краях
визначаємо з умов на краях  і
і  :
:

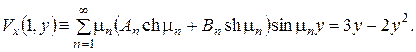
- 53 -
Із першої рівності маємо 
 Розклавши праву частину другої рівності в ряд Фур’є по системі власних функцій
Розклавши праву частину другої рівності в ряд Фур’є по системі власних функцій 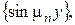 одержимо:
одержимо:
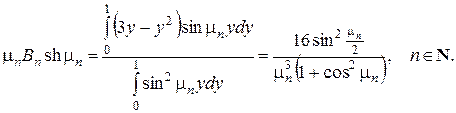
Підставивши знайдені коефіцієнти у ряд (12), одержимо розв’язок задачі (9) у вигляді

Аналоґічно розв’язується й задача (10):  , проте цього разу ЗШЛ будуємо для функції
, проте цього разу ЗШЛ будуємо для функції 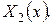 Одержимо:
Одержимо:


Звідси 

 (нуль теж є власним значенням). Відповідні функції
(нуль теж є власним значенням). Відповідні функції 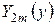 будуть
будуть

Тоді
 (13)
(13)
Коефіцієнти  і
і  визначаємо з умов на краях
визначаємо з умов на краях  і
і  :
:
 У правих частинах одержаних рівностей фіґурують тільки власні функції (маємо резонансний випадок), тому можна, не використовуючи розклад у ряд Фур’є, одразу прирівняти коефіцієнти при однакових власних функціях. Тоді з першої рівності будемо мати
У правих частинах одержаних рівностей фіґурують тільки власні функції (маємо резонансний випадок), тому можна, не використовуючи розклад у ряд Фур’є, одразу прирівняти коефіцієнти при однакових власних функціях. Тоді з першої рівності будемо мати 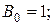

 З урахуванням знайдених коефіцієнтів
З урахуванням знайдених коефіцієнтів  із другої рівності одержимо:
із другої рівності одержимо: 
 а для всіх інших значень т
а для всіх інших значень т 
- 54 -
Підставивши знайдені коефіцієнти у ряд (13), одержимо розв’язок задачі (10) у вигляді
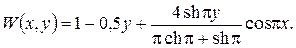
Поскільки вільний член у рівнянні задачі (11) справджує всі чотири крайові умови, то розв’язок цієї задачі можна було б шукати за допомогою методу власних функцій у вигляді ряду
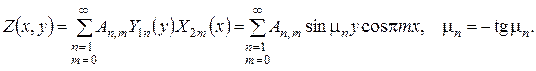
Проте, зваживши на простий вигляд вільного члена у рівнянні, легко побачити, що задача (11) аналоґічна до прикладу 3 і інтеґрується шляхом зведення неоднорідного рівняння до однорідного підстановкою
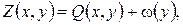
де допоміжна функція  повинна справджувати неоднорідне рівняння та умови на краях
повинна справджувати неоднорідне рівняння та умови на краях  та
та  , тобто повинна бути розв’язком крайової задачі
, тобто повинна бути розв’язком крайової задачі

Проінтеґрувавши цю задачу, одержимо  а для нової невідомої функції
а для нової невідомої функції 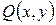 – однорідну задачу
– однорідну задачу
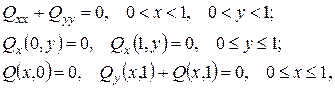
звідки очевидно, що  (див. приклад 3). Отже, розв’язок задачі (11) буде
(див. приклад 3). Отже, розв’язок задачі (11) буде

Додавши знайдені розв’язки задач (9), (10) і (11), одержимо шуканий розв’язок вихідної крайової задачі:
 де
де 
Іноді без застосування методу Фур’є вдається проінтеґрувати й більш складні за (11) крайові задачі.
ПРИКЛАД 5. Проінтеґрувати крайову задачу:
- 55 -
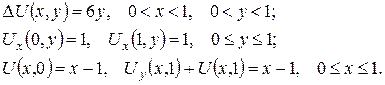
Розв’язання. На вигляд задача аналоґічна до прикладу 4, проте шукати її розв’язок вищенаведеним способом не можна, поскільки в дочірніх задачах крайові умови стануть неузгодженими. Отже, застосовуємо інший спосіб (див. приклад 3): покладемо

де  – деякий частинний розв’язок рівняння
– деякий частинний розв’язок рівняння
 (14)
(14)
котрий потрібно підібрати таким чином, щоб до одержаної задачі для  був застосовний метод Фур’є. При цьому бажано, щоб одержана нова задача була максимально простою.
був застосовний метод Фур’є. При цьому бажано, щоб одержана нова задача була максимально простою.
Спробуємо виконати ці умови для нашого прикладу. Очевидно, що довільна функція вигляду  де А, В, С – довільні сталі, є розв’язком рівняння (14). Виберемо тепер сталі А, В, С таким чином, щоб справдити хоча б деякі з чотирьох крайових умов. Маємо:
де А, В, С – довільні сталі, є розв’язком рівняння (14). Виберемо тепер сталі А, В, С таким чином, щоб справдити хоча б деякі з чотирьох крайових умов. Маємо:

Легко бачити, що при В=1, С=-1 та А=-2 справджуються усі чотири крайові умови. Отже, беремо  . Тоді для
. Тоді для  одержимо задачу:
одержимо задачу:

звідки  , а тому
, а тому

Розглянемо задачу Неймана для рівняння Лапласа у прямокутнику 

Умова стаціонарності теплового поля для такої задачі має вигляд
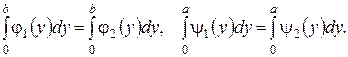
- 56 -
При невиконанні хоча б однієї з цих умов задача розв’язку не має. Проте у випадку задачі Неймана для рівняння Пуассона іноді вдається підібрати частинний розв’язок рівняння таким чином, щоб крайові умови стали узгодженими.
ПРИКЛАД 6. Проінтеґрувати крайову задачу

Розв’язання. Очевидно, що умова стаціонарності теплового поля тут не виконується, поскільки  Тому розв’язок потрібно шукати у вигляді
Тому розв’язок потрібно шукати у вигляді  де
де  – деякий частинний розв’язок рівняння
– деякий частинний розв’язок рівняння 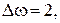 причому для
причому для  крайові умови повинні стати узгодженими. Шляхом підбору знаходимо, наприклад,
крайові умови повинні стати узгодженими. Шляхом підбору знаходимо, наприклад,  тоді для
тоді для  одержимо задачу
одержимо задачу

Тут крайові умови є узгодженими, і задача має очевидний розв’язок

(як відомо, розв’язок внутрішньої задачі Неймана завжди визначається з точністю до сталого доданка). А тоді