Итак, подошли к реализации передаточных функций объектов, проделав последовательность
Эксперимент 
передаточная функция последовательное соединение различных динамических звеньев.
При синтезе объектов с требуемыми динамическими характеристиками возникает задача реализации их передаточных функций пассивными или активными четырехполюсниками постоянного тока.
Последние содержат пассивные двухполюсники.
Пассивные двухполюсники и четырехполюсники постоянного тока – это электрические цепи из резисторов (активных сопротивлений), конденсаторов и индуктивностей.
Рассмотрим некоторые методы определения [11] электрических схем и параметров двухполюсников и четырехполюсников, состоящих из резисторов и конденсаторов, по передаточным функциям, которые они должны иметь.
Любая передаточная функция может быть реализована пассивным двухполюсником или четырехполюсником из резисторов и конденсаторов с точностью до постоянного множителя.
4.3.1. Разложение передаточной функции активного четырехполюсника
Схема активного четырехполюсника представлена на рисунке 4.11.
Такие четырехполюсники состоят из электронных усилителей и цепей из резисторов, конденсаторов и индуктивностей.
В общем случае четырехполюсник содержит входную цепь с импедансом 
и цепь с импедансом 
, которая охватывает усилитель с отрицательной обратной связью.
Обычно используют операционный усилитель с весьма большим передаточным коэффициентом. Тогда передаточная функция четырехполюсника определяется выражением
. (4.18)
Для синтеза двухполюсника активного четырехполюсника передаточную функцию 
, которую он должен иметь, нужно представить в соответствии с выражением (4.18) в виде отношения
,
где 
- операторные выражения полного сопротивления двухполюсника прямой о обратной цепи соответственно.
Полное сопротивление 
может быть реализовано в виде RC–двухполюсника только если оно удовлетворяет следующим условиям:
а) функция 
- рациональная дробь, у которой степень числителя равна или на единицу меньше степени знаменателя;
б) полюсы (корни полинома знаменателя) и нули (корни полинома числителя) функция - простые, действительные, отрицательные и перемежаются между собой, т. е. между двумя соседними полюсами находится нуль и наоборот;
в) наименьшим по абсолютному значению является полюс, он может равняться нулю;
г) наибольшим по абсолютному значению является нуль; он конечен, если степень числителя функции 
равна степени знаменателя.
В ряде случаев реализуемые значения 
удается составить по формулам
,
где 
- полиномы соответственно числителя и знаменателя функции 
.
Полином 
выбирают так, чтобы 
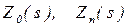удовлетворяли условиям реализуемости, он может содержать, в частности, двучлены из полиномов .
4.3.2. Способы синтеза двухполюсников
Схему и параметры RС - двухполюсника можно найти различными способами.
К схемам с наименьшим числом элементов приводят следующие способы.
1 способ .Разложени е на простые дроби
Пусть сопротивление , удовлетворяющее ранее перечисленным условиям, можно разложить на простые дроби
. (4.19)
Здесь
(4.20)
где 
.
Каждый член разложения (4.19) можно реализовать простыми RС – двухполюсниками из числа представленных ниже в таблице.
Таблица 4.2. RС – схемы и их полные сопротивления
   RC - схема
| |||
| Полное сопротивление z(s) | 
| 
| 
|
Последовательное соединение таких двухполюсников образует RС – двухполюсник, реализующий заданное полное сопротивление .
2 способ .Разложени е 
в непрерывную дробь
Члены полинома числителя и знаменателя функции нужно расположить по убывающим степеням s, после чего функцию можно разложить в непрерывную дробь.
Пусть степени числителя и знаменателя одинаковы и равны m. Тогда нужно определить первый член частного и результат записать так:
(4.21)
Далее нужно найти первый член частного 
, которая будет содержать s, т.к. степень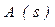 
на единицу выше степени 
, т.е.:
. (4.22)
Подставив (4.22) в (4.21), получим:
. (4.23)
Продолжение этого процесса приводит к искомому разложению
. (4.24)
Из разложения (4.24) следует, что есть полное сопротивление схемы, изображенной на рисунке 4.12.
 |
В случае, когда степень числителя на единицу меньше степени знаменателя, полное сопротивление
можно представить в виде:
и затем начать разложение его в непрерывную дробь. В результате получим:
. (4.25)
 |
По разложению (4.25) можно получить соответствующую RC-схему полного сопротивления для рассматриваемого случая:
Пример
Активный четырехполюсник постоянного тока, выполняемый по схеме, представленной на рисунке 4.11, должен иметь следующую передаточную функцию:
.
Выяснить, как должны быть выполнены соответствующие двухполюсники 
и 
.
Решение.
Преобразуем выражение требуемой передаточной функции.
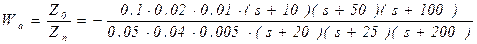
или
.
Ориентируясь на формулу 
, выберем передаточные функции двухполюсников так, чтобы они удовлетворяли условиям реализуемости:
.
Найдем схему и параметры двухполюсника обратной связи первым способом.
По формулам (4.13) и (4.14) имеем:
.
На основании таблицы 4.2 определим, что двухполюсник может быть выполнен по схеме, показанной на рисунке 4.14 со следующими элементами:
R=2 МОм; R1 = 150/25 = 6 МОм; с1 = 1/150» 0.0667 мкф.
Далее найдем схему и параметры двухполюсника прямой цепи тем же способом.
По выражениям (4.13) и (4.14) определим:
;
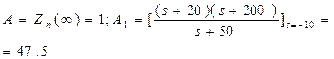На основании полученного разложения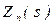 
и таблицы 4.2 схема двухполюсника будет иметь вид, представленный на рисунке 4.15.
Определим значения ее элементов:
R1 = 47.5/10 = 4.75 МОм;
с1 = 1/47.5» 0.0211 мкф;
R2 = 112.5/50 = 2.25 МОм;
с2 =1/112.5» 0.0089 мкф; R = 1 МОм.
