3.2.1. Понятие системы
Базовым понятием математического моделирования является понятие системы.
Система в широком смысле – эквивалент понятия математической модели [6] и задается парой множеств 
(
- множество входов, 
- множество выходов) и отношением на 
, формализующем связь (зависимость) между входами и выходами.
Системе присущи следующие атрибуты (свойства):
1. Целостность (единство). Это означает, что система отделена от внешней среды; среда может оказывать на нее действие через входы и воспринимать отклик (реакцию) на эти действия через выходы.
2. Структуированность. Означает, что система разделена внутри на несколько подсистем, связанных и взаимодействующих между собой так же, как целая система взаимодействует с внешней средой.
3. Целенаправленность. Данное свойство требует задания некоторой цели, достижение которой говорит о правильной работе системы.
Под приведенное формальное определение системы подпадают практически все виды математических моделей систем.
Как систему можно трактовать любой преобразователь входных данных в выходные (“черный ящик”) (рисунок 3.1, а).
Системой можно назвать процесс решения задачи. При этом входами будут являться исходные данные, выходами – результаты, а целью - правильное решение (рисунок 3.1, б). Такой подход к системе подчеркивает ее целенаправленность и ведет свое происхождение от исследования операций – научной дисциплины, занимающейся разработкой количественных методов обоснования решений. Основное понятие здесь - операция: действие, которое подвергается исследованию (проектирование, управление, экономическая деятельность и т.д.).
Операция соответствует некоторой системе. Входами этой системы являются элементы принимаемого решения о проводимой операции, выходами - результаты проведения операции (показатели ее эффективности (рисунок 3.1, в)).
Необходимо отметить, что функционирование системы – это процесс, разворачивающийся во времени, т.е. множества возможных входов и выходов - это множества функций времени со значениями соответственно в множествах :
,
где 
- множество моментов времени, на котором рассматривается система.
Система называется функциональной (определенной), если каждой входной функции 
соответствует единственная выходная функция 
.
Иначе система называется неопределенной. Неопределенность обычно возникает из-за неполноты информации о внешних условиях работы системы.
Важным свойством, присущим реальным системам, является причинность. Она означает, что если входные функции 
и 
совпадают при 
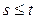, т.е. 
при 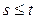, то соответствующие выходные функции удовлетворяют условию 
, т.е. “настоящее не зависит от будущего при заданном прошлом”.
Числовые величины, связанные с системой, делятся на переменные и параметры.
Параметры – это величины, которые можно считать постоянными на промежутке времени рассмотрения системы. Остальные числовые величины являются переменными.
Значения переменных и параметров определяют количественную информацию о системе. Оставшаяся информация, т.е. качественная, определяет структуру системы. Следует отметить, что различие между параметрами и переменными, а также между параметрами и структурой может быть условным, однако оно полезно в методическом отношении.
3.2.2. Этапы системного анализа и декомпозиция
Системный анализ в широком смысле – это методология постановки и решения задач построения и исследования систем, тесно связанная с математическим моделированием. В более узком смысле системный анализ – это методология формализации сложных задач. Это целенаправленная творческая деятельность человека, на основе которой обеспечивается представление исследуемого объекта в виде системы. Системный анализ характеризуется упорядоченным составом методических приемов исследования.
Существует понятие “системный подход”, под которым подразумеваются традиции его применения с исследованиями, проводимыми многоаспектно, комплексно, с разных сторон изучая предмет или явление. Этот подход предполагает, что все частные задачи, решаемые на уровне подсистем, должны быть увязаны между собой и должны решаться с позиции целого.
А системный анализ – это более конструктивное направление, содержащее методику разделения процессов на этапы и подэтапы, систем - на подсистемы, целей - на подцели и т.д.
 |
В системном анализе выработана определенная последовательность действий (этапов) при постановке и решении задач, которую называют алгоритмом (методикой) системного анализа (рисунок 3.2).
Эта методика помогает более осмысленно и грамотно ставить и решать прикладные задачи. Если на каком-то этапе возникают затруднения, то необходимо вернуться на один из предыдущих этапов и изменить (модифицировать) его. Если и это не помогает, то это значит, что задача оказалась слишком сложной и ее необходимо разбить на несколько более простых подзадач, т.е. провести декомпозицию. Каждую из полученных подзадач решают по той же методике.
 |
Результатом этого процесса является структуризация: исходная система приобретает многоуровневую структуру. Соответствующая структура возникает и в множестве подцелей; она называется деревом целей, поскольку представляет собой граф типа дерева (см рисунок 3.3).
Примечание.
Графом называется пара 
, где 
- конечное множество вершин, а 
- бинарное отношение на 
. Если 
, тогда и только тогда, когда 
, то граф называется неориентированным, иначе – ориентированным. Пары называются дугами (ребрами), а элементы 
множества - вершинами графа.
Теория графов является естественным математическим аппаратом описания сложных систем, поскольку каждой сложной системе ставится в соответствие граф (структурный), вершинами которого являются подсистемы, а дугами – имеющиеся между ними связи. Если связи направленные (т.е. наличие связи 
означает, что воздействие 
на 
не вызывает обратного воздействия или им можно пренебречь), то граф системы является ориентированным (направленным). К этому классу относятся, например, структурные схемы (графы-схемы) систем автоматического управления. У других систем влияние связанных подсистем обоюдно, и они описываются неориентированными графами (например, сложные электрические и электронные схемы).
3.2.3. Экспертные оценки
На начальных этапах алгоритмизации решаемой задачи исследователю, как правило, приходится иметь дело с неточной, неполной и субъективной информацией. Поэтому важно уметь пользоваться существующими методами ее сбора, согласования и обработки. Наиболее развитыми из подобных методов на сегодня являются методы экспертных оценок.
Экспертные оценки включают в себя специально разработанные приемы сбора, согласования и математическую обработку сведений, получаемых от экспертов или целенаправленно сформированной группы экспертов.
Использование таких оценок является одним из наиболее простых, доступных и достаточно надежных способов получения и дальнейшего использования априорной информации. Результаты, полученные с привлечением методов экспертных оценок, оказываются весьма полезными на различных стадиях разработки эскизного проекта и технического задания.
Экспертные оценки следует трактовать шире, чем просто сбор и усреднение произвольно собранных точек зрения, что действительно является некорректным. Результаты экспертизы следует рассматривать как способ получения дополнительной информации, позволяющей уменьшить неопределенность в решении задач.
Существует большое количество методов сбора и последующей обработки субъективной информации, которой располагают опытные специалисты, выбранные в качестве экспертов. Классификация методов получения экспертных оценок показана на рисунке 3.4.
Из анализа представленных на рисунке 3.4 методов достаточно ясно следует, что использование любого из них имеет свои преимущества и недостатки. И использование того или метода зависит от того, чем располагает исследователь при решении поставленной задачи.
