5.2.1. Погрешности измерений
Датчик в определенных условиях эксплуатации подвергается воздействию не только измеряемой величины, но и других физических величин, именуемых влияющими, к которым чувствителен датчик.
В идеальном случае имеет место связь
,
а фактически имеет место
, (5.3)
где m – измеряемая величина;
gi – величины, влияющие на датчик.
Для уменьшения погрешности датчиков, очевидно, необходимо:
- снизить значения влияющих величин gi путем соответствующей защиты датчика;
- стабилизировать влияющие величины gi и градуировать датчик с учетом этих величин.
Случайные ошибки измерений приводят к разбросу результатов при повторении измерений.
Статистическая обработка результатов позволяет определить наиболее вероятные значения измеряемой величины и оценить пределы его погрешности.
Статистическую обработку осуществляют по выражениям:
- среднее значение измеряемой величины 
; (5.4)
- разброс результатов, выраженный через его среднеквадратическое отклонение (СКО)
, (5.5)
где n - количество измерений.
Вероятность нахождения случайно измеряемой величины m в некотором диапазоне изменения находится по выражению
, (5.6)
где 
- плотность распределения величины (плотность вероятности).
В случае нормального закона распределения [4] плотность определяется по зависимости:
. (5.7)
Наиболее вероятная величина m равна 
, а вероятность появления результатов измерения в указанных ниже пределах равна:
(5.8)
Очевидно, чем меньше СКО 
, тем выше сходимость результатов, а отсюда можно ограничиться и меньшим количеством измерений величины m.
5.2.2. Чувствительность датчиков
Чувствительность датчика S является определяющим параметром при выборе датчика.
Чувствительность определяется по зависимости:
, (5.9)
где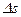 
- вариации сигнала на выходе датчика;
- изменение измеряемой величины;
- некоторое значение измеряемой величины, вблизи которого производится измерение.
Единицы измерения зависят от принципа работы датчика и природы измеряемой величины.
Например, для терморезистора размерностью является [Ом / 0С], а для термопары - [мкВ / 0С].
В зависимости от частоты изменений измеряемой величины существует два режима работы датчиков:
- статический, если измеряемая величина постоянная или меняется медленно;
- динамический, если измеряемая величина меняется быстро.
Отношение величины на выходе 
к соответствующей измеряемой величине называют статическим коэффициентом преобразования
, (5.10)
где 
- рабочая точка.
Это отношение 
не зависит от рабочей точки и совпадает с чувствительностью 
только в том случае, когда статическая характеристика является прямой, проходящей через начало координат.
В наиболее общей форме связь между величинами и 
представляют собой дифференциальные уравнения.
Зависимость чувствительности в динамическом режиме от частоты f, т.е. 
, является частотной характеристикой датчика.
Частотные характеристики связаны с порядком дифференциального уравнения, описывающего работу датчика.
Частотная характеристика датчика первого порядка
Такой датчик описывается дифференциальным уравнением вида
, (5.11)
где A, B – постоянные коэффициенты.
Если измеряемая величина меняется по гармоническому закону вида
, (5.12)
где 
- амплитуда величины, а 
- круговая частота, то выходная величина датчика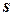 
может быть определена по зависимости
, (5.13)
где 
- амплитуда выходной величины датчика, 
- сдвиг фазы выходного сигнала датчика относительно входного.
В комплексной форме вместо выражений (5.12) и (5.13) соответственно имеем:
, (5.14)
. (5.15)
Частотная характеристика датчика второго порядка
В этом случае датчик описывается дифференциальным уравнением вида
, (5.16)
где A, B, С – постоянные коэффициенты.
Как пример в качестве такого датчика рассмотрим акселерометр, который служит для определения ускорений движения объекта.
Схема акселерометра представлена на рисунке 5.7, где M, R - масса и пружина.
Эта система помещена в корпус, в котором находится датчик положения и схема вывода наружу электрического сигнала, регистрирующего движение чувствительной массы относительно продольной оси корпуса.
Введем обозначения:
h0 – координата некоторой точки «а» корпуса;
h – текущее положение точки b массы, выбранной так, что положению покоя соответствует h= h0;
F - коэффициент силы вязкого трения, пропорциональной перемещению массы относительно корпуса;
C – коэффициент восстанавливающей силы пружины, пропорциональной перемещению массы M относительно корпуса.
Уравнение движения массы в общем виде можно записать
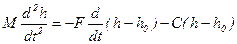. (5.17)
Вторичный преобразователь чувствителен только к относительному перемещению 
.
Тогда уравнение (5.17) можно переписать
, (5.18)
где 
- ускорение массы, направленное вдоль оси акселерометра.
Очевидно, что при 
в установившемся режиме имеет место 
, (5.18)
т.е. перемещение массы пропорционально ее ускорению.
5.2.3. Быстродействие датчика
Правильные измерения датчика обеспечиваются в установившемся режиме его работы.
Установившемуся режиму предшествует переходный процесс.
Время переходного процесса датчика можно определить решением дифференциального уравнения, описывающего этот датчик.
Быстродействие – это параметр датчика, позволяющий оценить, как выходная величина следует во времени за изменяющейся измеряемой величиной.
Параметр, используемый для количественного описания быстродействия – это время установления, т.е. интервал времени, который должен пройти после резкого ступенчатого воздействия до достижения фиксированной величины 
относительно установившегося значения.
Время установления нужно определять, указывая величину , которой оно соответствует 
.
Покажем, как определять время установления для датчиков, описываемых уравнениями первого и второго порядка.
Датчик первого порядка
При ступенчаом изменении величины по закону
(5.19)
решение дифференциального уравнения вида (5.11)
(5.20)
с начальными условиями
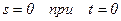(5.21)
имеет вид
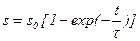, (5.22)
где 
- величина 
в установившемся режиме;
- постоянная времени датчика.
Время установления 
можно определить из (5.22) после соответствующих элементарных преобразований:
(5.23)
Датчик второго порядка
В этом случае решается дифференциальное уравнение вида (5.16)
(5.23)
с начальными условиями
(5.24)
Для установившегося режима имеет место 
.
В этом случае переходный режим описывается синусоидой с амплитудой, убывающей по экспоненте:
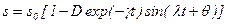, (5.25)
где
. (5.26)
Время установления опеделяется из последних выражений выражений (5.25) и (5.26) аналитическим или гафоаналитическим способом. В виду громоздкости аналитического способа наиболее эффективным является второй.
