Если функция  определена и непрерывна на любом отрезке [ a,b ], то несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода называется интеграл:
определена и непрерывна на любом отрезке [ a,b ], то несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода называется интеграл:
 или
или  , или
, или
 , с – произвольное число.
, с – произвольное число.
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если предел не существует или бесконечен, то несобственный интеграл называется расходящимся.
Теоремы о сходимости и расходимости:
1. Если на промежутке  непрерывные функции
непрерывные функции  и
и 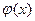 удовлетворяют условию:
удовлетворяют условию:  , то из сходимости интеграла
, то из сходимости интеграла  следует сходимости интеграла
следует сходимости интеграла  , а из расходимости интеграла
, а из расходимости интеграла  следует расходимость интеграла
следует расходимость интеграла  («признак сравнения»).
(«признак сравнения»).
2. Если при 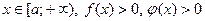 и существует конечные предел
и существует конечные предел  , то интегралы
, то интегралы  и
и  сходятся или расходятся одновременно («предельный признак сравнения»).
сходятся или расходятся одновременно («предельный признак сравнения»).
3. Если сходится интеграл  , то сходится и интеграл
, то сходится и интеграл  , который в этом случае называется абсолютно сходящимся.
, который в этом случае называется абсолютно сходящимся.
Примеры:
1.  - не существует
- не существует  несобственный интеграл расходится.
несобственный интеграл расходится.
2.  - интеграл сходится.
- интеграл сходится.
Несобственные интегралы второго рода (интеграл от разрывной функции)
Если функция  непрерывна на промежутке
непрерывна на промежутке  и имеет разрыв II-го рода при
и имеет разрыв II-го рода при  , то несобственным интегралом неограниченной функции или несобственным интегралом второго родва называется интеграл:
, то несобственным интегралом неограниченной функции или несобственным интегралом второго родва называется интеграл: 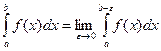 или
или  , если функция терпит бесконечный разрыв в точке
, если функция терпит бесконечный разрыв в точке  .
.
Если функция 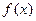 терпит разрыв II-го рода во внутренней точке
терпит разрыв II-го рода во внутренней точке  , то несобственным интегралом второго рода называют интеграл:
, то несобственным интегралом второго рода называют интеграл:  .
.
Замечание: внутренних точек разрыва II-го рода внутри отрезка может быть несколько.
Теоремы о сходимости и расходимости:
1. Если на промежутке 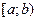 функции
функции 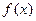 и
и  непрерывны, при
непрерывны, при  терпит разрыв II-го рода и удовлетворяют условию:
терпит разрыв II-го рода и удовлетворяют условию:  , то из сходимости интеграла
, то из сходимости интеграла  следует сходимости интеграла
следует сходимости интеграла  , а из расходимости интеграла
, а из расходимости интеграла  следует расходимость интеграла
следует расходимость интеграла  («признак сравнения»).
(«признак сравнения»).
2. Пусть функции 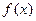 и
и  непрерывны на промежутке
непрерывны на промежутке 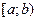 и в точке
и в точке  терпит разрыв II-го рода. Если существует предел
терпит разрыв II-го рода. Если существует предел  , то интегралы
, то интегралы  и
и  сходятся или расходятся одновременно («предельный признак сравнения»).
сходятся или расходятся одновременно («предельный признак сравнения»).
3. Если функция 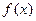 , знакопеременная на отрезке
, знакопеременная на отрезке  , имеет разрыв в точке
, имеет разрыв в точке  , и несобственный интеграл
, и несобственный интеграл  сходится, то сходится и интеграл
сходится, то сходится и интеграл  .
.
Задания для самопроверки №2
Вычислить:
1.  Ответ: 6-2ln4
Ответ: 6-2ln4
2.  Ответ:
Ответ: 
3. 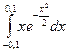 Ответ: 0
Ответ: 0
4.  Ответ:
Ответ: 
5.  Ответ:
Ответ: 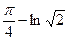
6.  Ответ:
Ответ: 
7.  Ответ: π
Ответ: π
8. Исследовать на сходимость несобственные интегралы:
a)  Ответ: сходится
Ответ: сходится
b)  Ответ: расходится
Ответ: расходится
c)  Ответ: сходится
Ответ: сходится
d)  Ответ: расходится
Ответ: расходится
Геометрические приложения определенного
Интеграла
1. Вычисление объём тела по известным площадям параллельных сечений
 Пусть тело, заключеное между двумя плоскостями x=a и x=b, имеет площадь сечения S(x) при
Пусть тело, заключеное между двумя плоскостями x=a и x=b, имеет площадь сечения S(x) при  , проведенного перпендикулярно к оси Ох, и которое является известной и непрерывной изменяющейся при изменении х.
, проведенного перпендикулярно к оси Ох, и которое является известной и непрерывной изменяющейся при изменении х.
Тогда объем этого тела вычисляется по формуле  .
.
2. Объёмы тел вращения
Пусть кривая, задана уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [ a, b ]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.

|
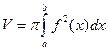 , где V – объем тела, полученного вращением криволинейной трапеции 0 £ y £ f(x),
, где V – объем тела, полученного вращением криволинейной трапеции 0 £ y £ f(x),
a £ x £ b вокруг оси Ох.
|

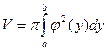 , где V – объем тела, полученного вращением криволинейной трапеции 0£ x £ j(y),
, где V – объем тела, полученного вращением криволинейной трапеции 0£ x £ j(y),
c £ y £ d вокруг оси ОУ.
3. Площади плоских фигур, длины дуг кривых, площадь поверхности тела вращения рассмотрим в таблице 8.
Таблица 8.
| В прямоугольных координатах | В полярных координатах | |||
y=f(x) на  или
x=φ(y)на или
x=φ(y)на 
|  
|   . .
| ||
| Площадь плоских фигур | ||||
 или или

| 
| 
| ||
| Длины дуг кривых | ||||
 или или

| 
| 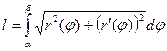
| ||
| Вычисление площади поверхности вращения | ||||

| 
| 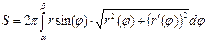
| ||
Примеры:
1. Вычислить площади фигур, ограниченных графиками функций:
а) 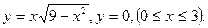
Решение:


б)  y=2 (
y=2 ( ).
).
Решение:

 .
.
2. Вычислить длины дуг кривых, заданных уравнениями.
а) 
Найдём сначала производную


б) 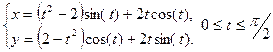
Найдём производные


в) 
Найдём производную 
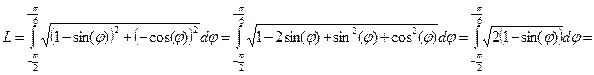

3. Найти площадь поверхности, образованной вращением кардиоиды  вокруг полярной оси (рис. см. приложение №1).
вокруг полярной оси (рис. см. приложение №1).
Решение:
 ,
,  Þ
Þ 

=  =
=  =
=  (ед. кв.)
(ед. кв.)
4. Найти объем тела, образованного вращением эллипса  вокруг оси Ох.
вокруг оси Ох.
Решение:
Так как эллипс симметричен относительно осей координат, то достаточно найти половину искомого объема и полученный результат удвоить.  =
=  =
= 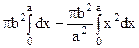 =
=  = =
= = 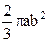 . Следовательно
. Следовательно 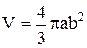 .
.
5.Найти площадь поверхности шара радиуса R, рассматривая его как тело вращения.
Решение.
Поверхность шара может быть образована вращением дуги полуокружности. Рассмотрим разные варианты задания уравнения окружности:
1) Окружность задана в декартовых координатах:
а) полуокружность  ,
,  вращение вокруг оси Ох.
вращение вокруг оси Ох.
Применяем формулу: 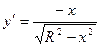 ,
,  ,
,
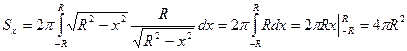 .
.
б) полуокружность  ,
, 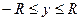 вращение вокруг оси Оу.
вращение вокруг оси Оу.
Применяем формулу: 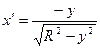 ,
,  ,
,
 .
.
2) Окружность задана параметрическими уравнениями:  .
.
Применяем формулу: 
 . Следовательно,
. Следовательно,  .
.
3) Окружность задана в полярных координатах.
Применяем формулу:  .
.
Следовательно,  .
.




