Пример: 
.
2. Замена переменных.
Пусть задан интеграл 
, где f(x) – непрерывная функция на отрезке [ a, b ]. Введем новую переменную в соответствии с формулой x = j(t).
1) j(a) = а, j(b) = b;
2) j(t) и j¢(t) непрерывны на отрезке [ a, b ];
3) f(j(t)) определена на отрезке [ a, b ], то 
.
Тогда 
Пример:
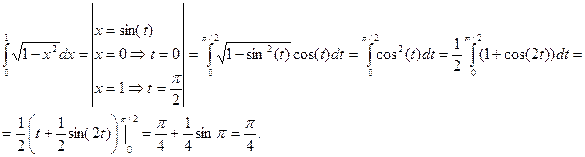
3. Интегрирование по частям.
Формула имеет вид: 
.
Пример: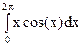 
= 
= 
=
= 
+ 
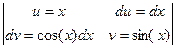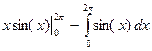=0.
Приближенное вычисление определенного
Интеграла
Потребность в приближенном вычислении интеграла возникает тогда, когда не существует или неизвестен метод отыскания точного значения интеграла, и тогда, когда этот метод известен, но неудобен.
Формула прямоугольников
Пусть на отрезке [ a, b ] задана непрерывная функция f(x).
Разобьем отрезок [ a, b ] на n равных частей, длины которых равны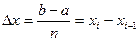 
, где x1, x2, … xn – точки разбиения. Тогда можно записать, что 
.
При таком разбиении имеем прямоугольники, площадь которых равна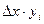 
, где 
, а 
– некоторая точка на отрезке, которая в частности выбирается середина отрезка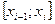 
.
Тогда сумма площадей всех прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение определенного интеграла и называемое общей формулой прямоугольников:
.
Формула трапеций
Эта формула является более точной по сравнению с формулой прямоугольников.
Подынтегральная функция в этом случае заменяется на вписанную ломаную. Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций.
Замечание: чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.
Площади вписанных трапеций вычисляются по формулам:
;
.
После приведения подобных слагаемых получаем формулу трапеций:
Формула парабол (формула Симпсона или квадратурная формула)
Данный метод основан на разбиении дуги линии f(x), соответствующую [ a, b ], дугами парабол, что позволяет получить более точную формулу приближенного вычисления. Для этого разделим отрезок интегрирования [ a, b ] на четное число отрезков (2m).
Площадь криволинейной трапеции, ограниченной графиком функции f(x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси OY и проходящей через точки кривой, со значениями f(x0), f(x1), f(x2).
Для каждой пары отрезков построим такую параболу.
|
|
|
|
|
Уравнения этих парабол имеют вид
Ax2 + Bx + C,
где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
Для определения А, В, С имеется система уравнений:
(1)
Если обозначим 
и примем х0 = -h, x1 = 0, x2 = h, то 
(2)
Выразается S через величины (1): 
C учетом этого: 
.
Отсюда выражение (2) примет вид: 
Тогда для каждой пары отрезков имеется:
...
Суммируя эти выражения, получаем формулу называемую формулой Симпсона: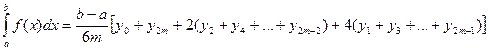 
Пример:
Вычислим приближенное значение определенного интеграла 
с помощью формулы Симпсона и формулы трапеций, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
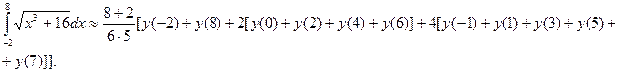
| m | |||||||||||
| x | -2 | -1 | |||||||||
| f(x) | 2.828 | 3.873 | 4.123 | 4.899 | 6.557 | 8.944 | 11.874 | 15.232 | 18.947 | 22.978 |
Точное значение этого интеграла: 91.173.
Для сравнения применим к этой же задаче формулу трапеций.
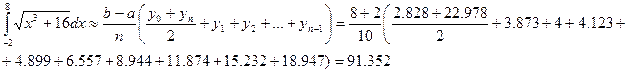
Несобственные интегралы
