Основные понятия неопределенного интеграла
Неопределенным интегралом функции f(x) называется множество всех первообразных функций F(x) + C.
Записывается это так: 
Первообразной функцией для функции f(x) на промежутке (a; b) называется такая функция F(x), производная которой равна f(x) на рассматриваемом промежутке, то есть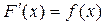 
.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Имеет место теорема: Две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от друга в этом промежутке на некоторое постоянное слагаемое.
Функция f(x) называется непрерывной на отрезке [ a, b ], если 1) она определена на этом множестве; 2) непрерывна в каждой точке этого отрезка, то есть 
справедливо равенство 
, где 
.
Теорема (условие существования неопределенного интеграла). Всякая непрерывная на отрезке [ a, b ] функция имеет на этом промежутке неопределенный интеграл.
Основные теоремы (свойства неопределенного интеграла):
1. 
где C-const.
2. 
.
3. 
.
4. 
где u, v, w – некоторые функции от х.
5. 
6. (Инвариантность формулы интегрирования). Если 
, то и 
, где 
- произвольная функция, имеющая непрерывную производную.
Ниже приводится таблица основных интегралов, которые используются при вычислениях неопределенных интегралов различных функций. Верность этой таблицы проверяется непосредственно дифференцированием.
Таблица 1.
| Интеграл | Значение | Интеграл | Значение | ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
|
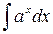
Основные методы интегрирования
Метод непосредственного интегрирования
Метод интегрирования основан на применении табличных интегралов, и называется непосредственным интегрированием. При этом данный интеграл может быть приведен к табличному с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.
Примеры:
a) 
b) 
с) 
.
Замена переменной
Этот метод интегрирования основан на введении новой переменной интегрирования. Приведем пример: пусть дана сложная функция f(x), где 
- функция имеющая непрерывную производную 
. Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем: 
.
Эта формула называется формулой замены переменной в неопределенном интеграле.
Примеры:
a) 
b) 
.
с) 
.
Первый вариант замены: = 
= 
Второй вариант замены:
= 
= 
d) 
. Первый вариант замены:
= 
Второй вариант замены: 
= 
= .
При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций: рациональных, тригонометрических и т.д. (интегрирование этих классов функций предложены в таблицах 3 – 7).
Интегрирование по частям
Этот метод интегрирования основан на применении формулы дифференцирования произведения d(uv)=udv+vdu и вычислении затем интеграла 
. Из этого равества получаем формулу интегрирования по частям: 
.
Примеры:
a) 
Интегирируется по частям: пусть 
; тогда 
, 
. Следовательно, 
.
Еще раз интегрируется по частям: пусть 
тогда 
. Получаем, 
.
b) 
Интегирируется по частям: пусть 
; тогда 
. Следовательно, 
.
c) 
Интегирируется по частям: пусть 
; тогда 
, 
. Следовательно, 
.
Получившийся интеграл вычисляется методом замены переменной:
. Тогда 
.
d) 
Пусть 
. Тогда 
.
Интегирируется по частям: пусть 
; тогда 
. Следовательно, 
.
e) 
Интегирируется по частям: пусть 
; тогда 
, . Следовательно, 
.
Обозначается, 
. Тогда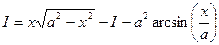 
.
Следовательно, 
.
f) 
Интегирируется по частям: пусть 
; тогда 
. Следовательно, 
.
g) 
Интегрируется по частям: пусть 
тогда 
. Следовательно, 
.
Еще раз интегрируется по частям: пусть 
тогда 
. Получается,
=
= 
.
Обозначается, 
. Тогда 
.
Следовательно, 
h) 
Интегрируется по частям: пусть 
тогда 
. Следовательно,
.
Еще раз интегрируется по частям: пусть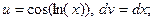 
тогда 
. Получается,
Обозначают, 
. Тогда 
Следовательно, 
k) 
Интегрируется по частям: пусть 
тогда 
.
Следовательно, 
Приведем в таблице 2 некоторые распространённые случаи использования метода интегрирования по частям.
Таблица 2.
| вид интеграла | метод интегрирования |
 ,
 ,
 .
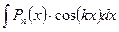| За u принимается многочлен  , а за dv все остальные подынтегральные выражения.
|
 ,
 ,
 ,
 ,
 .
| За dv принимается  , а за u все остальные подынтегральные выражения.
|
 ,
 ,
 ,
 .
| данные бесконечные интегралы, решаются как уравнения, после двукратного интегрирования по частям. |
,
 , a > 0.
| За dv принимается dх, а за u остальные подынтегральные выражения. |
Интегрирование рациональных дробей
Дробно-рациональной функцией называется функция вида: 
, где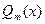 
- многочлен степени m, 
- многочлен степени n.
Замечание: Если m < n, то рациональную дробь называется правильной. Если m ³ n, то рациональную дробь называется неправильной.
Примеры:
a) 
= 
;
b) 
.
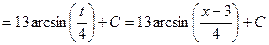c) 
d) 
.
Интеграл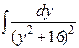 
вычисляется с помощью:
· рекуррентной формулы: Она выведена в курсе математического анализа: 
Следовательно,
.
· интегрирования по частям:
В таблице 3 приведены общие виды правильных рациональных дробей и способы их интегрирования с помощью замены переменной.
Таблица 3.
| № | подынтегральное выражение | преобразования | замена | dx |
| I. | 
| 
| 
| |
| II. | 
|
|
| |
| III. | 
| 
| 
| 
|
| IV. | 
| 
| 
|  и раскладывается на сумму двух интегралов
|
| V. | 
| 
|
|
|
и применяется рекуррентная формула 
|
m, n – натуральные числа (m ³ 2, n ³ 2) и D <0.
Подынтегральные выражения не вошедшие в таблицу 3 интегрируются с помощью метода неопределенных коэффициентов.
Теорема (метод неопределенных коэффициентов). Если 
- правильная рациональная дробь, где знаменатель имеет вид:
P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ) (причем множители типа x2+px+q неразложимы на действительные множители первой степени), то эта дробь может быть разложена на сумму простейших дробей:
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
Примеры:
a) 
= 
Подынтегральное выражение представляется в виде суммы простейших дробей 
.
После освобождения от знаменателей, получается:
.
Сгруппировываются члены с одинаковыми степенями:
В итоге получается:
b) 
.
Так как дробь неправильная, то выделяется целая часть:
6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x - 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
Следовательно,
Для нахождения корней уравнения 
применяем схему Горнера:
| коэффициенты перед x | |||||
| ре ше ние | – 4 | – 17 | |||
| – 2 | – | ||||
| – 2 | – 1 | – | – | ||
| 1/3 | – | – | – |
Получаются: 
.
Следовательно, корни этого уравнения: 3; -2; 1/3.
Отсюда 
.
Получившееся подынтегральное выражение раскладывается на элементарные дроби: 
Применяем метод произвольных значений, суть которого состоит в том, что в полученное выражение подставляем поочередно (по числу неопределенных коэффициентов) значения х. Для упрощения вычислений принимают точки, при которых знаменатель дроби равен нулю. В нашем случае: 3, -2, 1/3. Получаем:
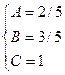
В итоге получаем:
= 
