Вычислить:
1.  Ответ:
Ответ: 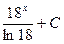
2.  Ответ:
Ответ: 
3.  Ответ:
Ответ: 
4.  Ответ:
Ответ: 
5.  Ответ:
Ответ: 
6.  Ответ:
Ответ: 
7.  Ответ:
Ответ: 
8. 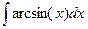 Ответ:
Ответ: 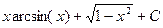
9.  Ответ:
Ответ: 
10.  Ответ:
Ответ: 
11. 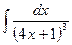 Ответ:
Ответ: 
12.  Ответ:
Ответ: 
13.  Ответ:
Ответ: 
14.  Ответ:
Ответ: 
15.  Ответ:
Ответ: 
16. 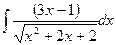 Ответ:
Ответ: 
17.  Ответ:
Ответ: 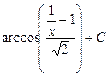
18.  Ответ:
Ответ: 
19.  Ответ:
Ответ: 
20.  Ответ:
Ответ: 
21.  Ответ:
Ответ: 
22.  Ответ:
Ответ: 
23.  Ответ:
Ответ: 
24.  Ответ:
Ответ: 
25. Используя метод интегрирования по частям, доказать, что:
а)  ;
;
b)  ;
;
c)  .
.
§2. Определенный интеграл
Основные понятия и методы решения
Определенного интеграла
Пусть на отрезке [a, b] задана непрерывная функция f(x) [см. § 1]. Разобьём отрезок [a, b] произвольным образом на п частей точками 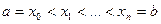 . На каждом отрезке
. На каждом отрезке  длины
длины  выберем произвольную точку
выберем произвольную точку  . Составим сумму
. Составим сумму  , называемую интегральной суммой для функции f(x) на отрезке [a, b].
, называемую интегральной суммой для функции f(x) на отрезке [a, b].
Определённым интегралом от функции f(x) на отрезке [a, b] называется число равное пределу интегральных сумм при стремлении к нулю
 максимальной из длин отрезков разбиения:
максимальной из длин отрезков разбиения: 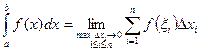 , этот предел конечен и не зависит от способов разбиения отрезка [a, b] на части и выбора точек
, этот предел конечен и не зависит от способов разбиения отрезка [a, b] на части и выбора точек  , на отрезках
, на отрезках  .
.
Определённый интеграл обозначается символом  , где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.
, где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.
Пусть на отрезке [ a, b ] задана непрерывная функция  . Фигура, ограниченная сверху графиком функции
. Фигура, ограниченная сверху графиком функции  , снизу – осью Ox, сбоку прямыми x=a и x=b, называется криволинейной трапецией.
, снизу – осью Ox, сбоку прямыми x=a и x=b, называется криволинейной трапецией.
Геометрический смысл определённого интеграла: определённый интеграл равен площади «криволинейной трапеции» ограниченной функцией  , осью О Y, и прямыми х=а и у=b.
, осью О Y, и прямыми х=а и у=b.
Теорема. Если функция f(x) непрерывна на отрезке [ a, b ], то определённый интеграл  существует.
существует.
Отметим, что если оставить постоянным нижний предел интегрирования а, а верхний х изменить так, что бы  , то величина интеграла будет изменяться. Интеграл:
, то величина интеграла будет изменяться. Интеграл:  , называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.
, называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.
Теорема ( Связь между неопределённым интегралом и определённым интегралами). Всякая непрерывная на отрезке [ a, b ] функция  имеет первообразную, равную интегралу
имеет первообразную, равную интегралу  , и тогда согласно определению неопределённого интеграла имеет место равенство
, и тогда согласно определению неопределённого интеграла имеет место равенство  .
.
Теорема (Ньютона – Лейбница). Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то  – это выражение известно под названием формулы Ньютона – Лейбница [4].
– это выражение известно под названием формулы Ньютона – Лейбница [4].
Основные свойства определенного интеграла:
1.  .
.
2.  .
.
3. 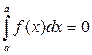 .
.
4. Если f(x) £ j(x) на отрезке [ a, b ] a < b, то  .
.
5. Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [ a, b ], то:  .
.
6. Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что  .
.
7. Для произвольных чисел a, b, c справедливо равенство: 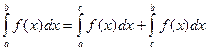 , где равенство выполняется, если существует каждый из входящих в него интегралов.
, где равенство выполняется, если существует каждый из входящих в него интегралов.
8.  .
.
9. 
Методы интегрирования определенного интеграла:




