Выбор оптимальной архитектуры

Как уже упоминалось (п. 3.1, теорема КАХН), количество нейронов входного слоя НС определяется размерностью N входного вектора , количество нейронов выходного слоя – размерностью M ожидаемого вектора . Определение минимального числа скрытых слоев основано на использовании свойств аппроксимирующих функций. Для непрерывного преобразования X®Y (см. теорему КАХН) достаточно иметь один скрытый слой с K =(2 N +1) нейронами, в случае дискретного преобразования необходимое число скрытых слоев возрастает до двух [1]. В практических реализациях ИНС как количество скрытых слоев, так и число нейронов в них могут отличаться от теоретически предлагаемых. За немногими исключениями, чаще всего используются НС, имеющие один (максимум – 2) скрытый слой. в котором К = N …3 N.

Определение оптимального числа К основано на способности ИНС к обобщению полученных знаний, т.е. выдаче правильных результатов при подаче на ее вход данных, не входящих непосредственно в обучающую выборку. Пример разделения множества данных, подчиняющихся правилу R, на обучающее L, контрольное V и тестовое G подмножества приведен на рис. 3.3. Элементы L и G должны быть типичными элементами множества R. Способность отображения сетью элементов L является показателем ее обученности и характеризуется погрешностью обучения 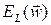, способность распознавания данных подмножества G показывает ее возможности обобщения знаний и описывается погрешностью обобщения . Для верификации качества обучения НС в составе L выделяется определенное подмножество контрольных данных V.

При обучении НС оказывается, что количество весов T_w сети (число степеней свободы) и число обучающих выборок р тесно связаны. Например, если бы целью обучения НС было только запоминание , тогда достаточно было бы p = T_w, однако такая сеть не будет обладать свойством обобщения и сможет только восстанавливать данные. Для обретения обобщающих свойств НС необходимо выполнение p > T_w, чтобы веса сети адаптировались не к уникальным выборкам, а к их статистически усредненным совокупностям. Наглядная графическая иллюстрация способности НС к обобщению показана на рис. 3.4 на примере аппроксимации одномерной функции двухслойной НС. Видно, как при избыточном числе нейронов и весов проявляется эффект гиперразмерности НС, когда минимизация 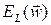на относительно малом числе обучающих выборок спровоцировала случайный характер значений многих весов, что при переходе к тестовым сигналам обусловила значительное отклонение фактических значений y_i от ожидаемых d_i (рис. 3.4 а). Уменьшение количества скрытых нейронов до оптимального значения (рис. 3.4 б) обеспечило и малую погрешность обучения, и высокую степень обобщения (малую ). Дальнейшее уменьшение К привело к потере НС способности восстанавливать обучающие данные (рис. 3.4 в).

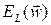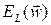Следует отметить, что длительность обучения по-разному влияет на значения и . Если погрешность монотонно уменьшается с увеличением числа итераций t, то снижение происходит только до определенного момента, после чего она начинает расти (рис. 3.5). Это означает, что слишком долгое обучение может привести к «переобучению» НС, которое выражается в слишком детальной адаптации весов к несущественным флуктуациям обучающих данных. Такая ситуация особенно заметна при использовании сети с излишним количеством весов. Для предотвращения перетренированности НС служит контрольное подмножество V, с помощью которого осуществляется оперативная проверка фактически набранного уровня обобщения .