Предложенный Н. Метрополисом в 1953 году, метод ИО представляет собой алгоритмический аналог физического процесса управляемого охлаждения, при котором кристаллизация расплава сопровождается глобальным уменьшением его энергии, причем допускаются ситуации кратковременного повышения энергетического уровня (например, при небольшом подогреве), способствующие выводу из ловушек локальных минимумов энергии, возникающих при реализации процесса. Классический алгоритм ИО можно представить следующим образом:
1. Определяем некоторую начальную переменную («температуру» T = Tmax и запускаем процесс обучения НС из некоторой начальной точки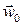 
.
2. Пока Т >0, повторяем L раз следующие шаги:
– выбираем новое решение 
из окрестности ;
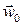– рассчитываем изменение целевой функции 
;
– если D£0, принимаем 
;
– если D>0, то вычисляем вероятность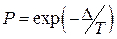 
, выбираем случайное число R Î(0,1) и, если R £ P, то , в противном случае (R > P) 
.
3. Уменьшаем температуру (Tk = rTk -1) с использованием коэффициента уменьшения r Î(0,1) и повторяем п. 2.
4. При снижении Т до нуля обучаем НС любым из представленных выше детерминированных методов.
Эффективность метода ИО сильно зависит от выбора Tmax, L и r. Величина Tmax определяется из предварительных имитационных экспериментов таким образом, чтобы обеспечить реализацию не менее 50% последующих случайных изменений решения. Выбор максимальных L и r для конкретных температурных уровней менее однозначен и должен учитывать динамику изменения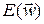 
в зависимости от количества выполненных циклов обучения. Общие рекомендации, вытекающие из компьютерных экспериментов, таковы: если время обучения ограничено, его лучше потратить на один процесс ИО с соответствующим удлинением циклов, если же моделирование может быть более длительным, статистически лучшие результаты достигаются при многократной реализации процесса ИО с большими (близкими к 1) значениями r и последующим выбором оптимального решения.
Таким образом, метод ИО наиболее эффективен для полимодальных комбинаторных проблем с большим числом возможных решений, например, для машины Больцмана, в которой каждое состояние системы (с различной вероятностью) считается допустимым. В общем же случае при решении наиболее распространенных задач обучения многослойных НС наилучшие результаты достигаются применением стохастических методов совместно с детерминированными алгоритмами локальной оптимизации.
