Все рассмотренные алгоритмы обучения НС связаны только с определением направления  на каждом шаге, но ничего не говорят о выборе коэффициента обучения
на каждом шаге, но ничего не говорят о выборе коэффициента обучения 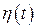 , хотя он оказывает огромное влияние на скорость сходимости: слишком малое значение
, хотя он оказывает огромное влияние на скорость сходимости: слишком малое значение 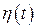 не позволяет минимизировать
не позволяет минимизировать 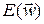 за один шаг в заданном направлении и требует повторных итераций, слишком большой шаг приводит к «перепрыгиванию» через минимум целевой функции и фактически заставляет возвращаться к нему. Существуют различные способы подбора h. Простейший из них основан на фиксации h=const на весь период оптимизации, практически используется только в АНС при обучении в режиме «online» и имеет низкую эффективность, поскольку никак не связан с величиной и направлением
за один шаг в заданном направлении и требует повторных итераций, слишком большой шаг приводит к «перепрыгиванию» через минимум целевой функции и фактически заставляет возвращаться к нему. Существуют различные способы подбора h. Простейший из них основан на фиксации h=const на весь период оптимизации, практически используется только в АНС при обучении в режиме «online» и имеет низкую эффективность, поскольку никак не связан с величиной и направлением  на данной итерации. Обычно величина h подбирается отдельно для каждого слоя НС, чаще всего с использованием соотношения
на данной итерации. Обычно величина h подбирается отдельно для каждого слоя НС, чаще всего с использованием соотношения
 (3.15)
(3.15)
где ni – количество входов i – го нейрона в слое.
Более эффективный способ – адаптивный выбор h с учетом динамики изменения 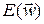 в процессе обучения, когда тенденция к непрерывному увеличению h сочетается с контролем суммарной погрешности
в процессе обучения, когда тенденция к непрерывному увеличению h сочетается с контролем суммарной погрешности 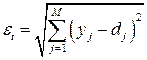 на каждой итерации. При этом
на каждой итерации. При этом
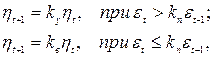 (3.16)
(3.16)
где ky, kв – коэффициенты уменьшения и увеличения ht соответственно, kn – коэффициент допустимого прироста погрешности e. Заметим, что реализация этой стратегии выбора h в NNT MATLAB 6.5 при kn = 1.41, ky = 0.7, kв = 1.05 позволила в несколько раз ускорить обучение многослойных НС при решении задач аппроксимации нелинейных функций.
Наиболее эффективный, хотя и наиболее сложный, метод подбора h связан с направленной минимизацией 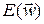 в заранее выбранном направлении
в заранее выбранном направлении  , когда значение ht подбирается так, чтобы новое решение
, когда значение ht подбирается так, чтобы новое решение 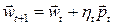 соответствовало минимуму
соответствовало минимуму 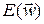 в направлении
в направлении  . Чаще всего определение оптимальной величины h связано с представлением
. Чаще всего определение оптимальной величины h связано с представлением 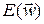 полиномом 2–го или 3–го порядка от h
полиномом 2–го или 3–го порядка от h
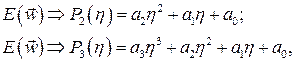 (3.17)
(3.17)
где для определения коэффициентов ai используют информацию о величине 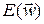 и ее производной в направлении
и ее производной в направлении  , а значения hопт получают из условия минимума Р 2(h) или Р 3(h) согласно
, а значения hопт получают из условия минимума Р 2(h) или Р 3(h) согласно 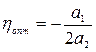 для Р 2(h) или
для Р 2(h) или  для Р 3(h).
для Р 3(h).
Эффективность алгоритмов обучения проверяется на стандартных тестах, к которым относятся задачи логистики (предсказания последующего значения хn +1 случайной последовательности по предыдущему значению xn), кодирования и декодирования двоичных данных, аппроксимации нелинейных функций определенного вида, комбинаторной оптимизации («задача коммивояжера») и т.п. Сравнение идет по количеству циклов обучения, количеству расчетов 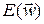 , чувствительности к локальным минимумам и т.д. Поскольку эти характеристики могут существенно отличаться в зависимости от характера тестовой задачи, то однозначный ответ на вопрос, какой алгоритм считать абсолютно лучшим, дать невозможно.
, чувствительности к локальным минимумам и т.д. Поскольку эти характеристики могут существенно отличаться в зависимости от характера тестовой задачи, то однозначный ответ на вопрос, какой алгоритм считать абсолютно лучшим, дать невозможно.
В качестве возможного примера сравнения эффективности рассмотренных методов обучения в табл. 3.1 представлены результаты обучения многослойного персептрона со структурой 1–10–1, предназначенного для аппроксимации одномерной функции на основе обучающей выборки из 41 элемента. Все алгоритмы обучения были реализованы в пакете дополнений NNT MATLAB, что послужило основой для получения объективных оценок. Видно, что наибольшую эффективность продемонстрировал АЛМ, за ним идут АПМ (BFGS) и АСГ. Наихудшие результаты (по всем параметрам) показал АНС, а эвристический алгоритм RPROP в этом примере был сравним с АПМ и АСГ. Заметим однако, что на основании более общих тестов был сделан вывод, что доминирующая роль АЛМ и АПМ снижается по мере увеличения размеров НС, и при числе связей больше 103 наиболее эффективным становится АСГ.
Таблица 3.1
| Алгоритм | Время, с | Кол-во циклов | Кол-во операций, (´10-6) |
| АНС с адаптируемым h | 57,7 | 2,50 | |
| Сопряженных градиентов | 19,2 | 0,75 | |
| АПМ типа BFGS | 10,9 | 1,02 | |
| Левенберга–Марквардта | 1,9 | 0,46 | |
| RPROP | 13,0 | 0,56 |






