Этот метод не использует информацию о 
, а направление поиска 
выбирается ортогональным и сопряженным всем предыдущим направлениям 
. Показано, что этим условиям удовлетворяет
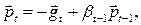(3.11)
где коэффициент сопряжения bt -1 играет важную роль, аккумулируя информацию о предыдущих направлениях поиска. Наиболее известны следующие правила определения bt -1:
(3.12)
Метод сопряженных градиентов имеет сходимость, близкую к линейной, он менее эффективен, чем АПМ, но заметно быстрее АНС. Благодаря невысоким требованиям к памяти и относительно низкой вычислительной сложности, АСГ широко применяется как единственно эффективный алгоритм оптимизации при значительном числе переменных (до нескольких десятков тысяч весов связей при обучении НС).
Эвристические методы обучения НС
Помимо алгоритмов обучения, использующих апробированные методы оптимизации нелинейной целевой функции, создано огромное количество алгоритмов эвристического типа, представляющих собой, в основном, модификацию АНС или АСГ. Подобные модификации связаны с внесением в них некоторых изменений, ускоряющих (по мнению авторов) процесс обучения ИНС. Как правило, эти методы не имеют серьезного теоретического обоснования, однако в них реализуется личный опыт работы авторов с нейронными сетями. К наиболее известным и эффективным эвристическим алгоритмам относятся:
- алгоритм Quickprop Фальмана, содержащий элементы, предотвращающие зацикливание в точках неглубоких локальных минимумов. Изменение весов на шаге t алгоритма осуществляется согласно
(3.13)
где первое слагаемое соответствует АНС, последнее – методу моментов, а средний член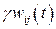 
предназначен для минимизации (g ~ 10–4) абсолютных значений весов вплоть до возможного разрыва соответствующих связей (при wij» 0). Важную роль в алгоритме Quickprop играет фактор момента aij (t), который подбирается индивидуально для каждого веса 
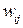и адаптируется к текущим результатам обучения;
- алгоритм RPROP Ридмиллера–Брауна, где при уточнении весов учитывается только знак градиентной составляющей, а ее значение отбрасывается. т.е.
(3.14)
Коэффициент обучения 
также подбирается индивидуально для каждого 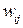с учетом изменения градиента на каждом шаге обучения. Предельные значения для алгоритма RPROP составляют hmin =10‑6 и hmax =50 соответственно. Заметим, что этот алгоритм позволяет значительно ускорить процесс обучения в тех случаях, когда угол наклона целевой функции невелик.
