В основе АПМ лежит ньютоновский алгоритм оптимизации с использованием вторых производных оценки, т.е. трех первых слагаемых в разложении (3.2). Для достижения минимума 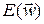 необходимо, чтобы
необходимо, чтобы  , т.е. дифференцированием (3.2) условие оптимальности можно получить в виде
, т.е. дифференцированием (3.2) условие оптимальности можно получить в виде  с очевидным решением
с очевидным решением
 (3.5)
(3.5)
однозначно указывающим направление, гарантирующее достижение на данном шаге минимальной 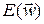 .
.
Применение (3.5) требует положительной определенности  на каждом шаге, что в общем случае практически неосуществимо, поэтому в известных реализациях алгоритма, как правило, вместо точного
на каждом шаге, что в общем случае практически неосуществимо, поэтому в известных реализациях алгоритма, как правило, вместо точного  используется его приближение
используется его приближение  , при котором гессиан или обратная ему величина модифицируется на величину некоторой поправки, вычис–ляемой по формулам Бройдена–Флетчера–Гольдфарба–Шенно (BFGS – метод) или Дэвидона–Флетчера–Пауэлла (DFP – метод). Если обозначить
, при котором гессиан или обратная ему величина модифицируется на величину некоторой поправки, вычис–ляемой по формулам Бройдена–Флетчера–Гольдфарба–Шенно (BFGS – метод) или Дэвидона–Флетчера–Пауэлла (DFP – метод). Если обозначить  то процесс уточнения матрицы V можно описать рекуррентными зависимостями: для BFGS – метода –
то процесс уточнения матрицы V можно описать рекуррентными зависимостями: для BFGS – метода –
 (3.6)
(3.6)
а для DFP – метода –
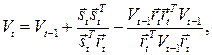 (3.7)
(3.7)
где в качестве начального значения обычно принимается V 0=1, а первая итерация выполняется в соответствии с АНС. Показано, что обеспечение с помощью (3.5), (3.6) положительной определенности гессиана на каждом шаге итерации действительно гарантирует решение проблемы оптимизации, причем метод BFGS менее чувствителен к различным погрешностям вычислительного процесса.
АПМ характеризуется более быстрой сходимостью, чем АНС, и именно он в настоящее время считается одним из наиболее эффективных методов оптимизации функций нескольких переменных, а, следовательно, и обучения ИНС. Его недостаток – это большие вычислительные затраты, связанные с необходимостью расчета и хранения в памяти n 2 элементов гессиана в каждом цикле, что при оптимизации функции с большим количеством переменных может стать серьезной проблемой. По этой причине метод применяется для не очень больших НС, имеющих не более тысячи взвешенных связей.
3.2.1.3. Алгоритм Левенберга–Марквардта (АЛМ)
Как и АПМ, АЛМ относится к ньютоновским методам оптимизации с заменой  приближенным
приближенным  , рассчитываемым на основе имеющейся информации о
, рассчитываемым на основе имеющейся информации о 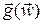 с учетом некоторого фактора регуляризации. Обозначая
с учетом некоторого фактора регуляризации. Обозначая
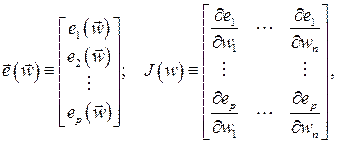 (3.8)
(3.8)
где  , вектор градиента
, вектор градиента 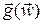 и матрицу
и матрицу  можно представить в виде
можно представить в виде
 (3.9)
(3.9)
где  – компоненты
– компоненты  с высшими производными относительно
с высшими производными относительно 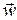 , которые в АЛМ аппроксимируются с помощью скалярного параметра Левенберга–Марквардта u, изменяющегося в процессе оптимизации таким образом, что
, которые в АЛМ аппроксимируются с помощью скалярного параметра Левенберга–Марквардта u, изменяющегося в процессе оптимизации таким образом, что
 (3.10)
(3.10)
В начале обучения, когда значения  далеки от решения, используют
далеки от решения, используют  , т.е.
, т.е.  и
и  , однако по мере уменьшения погрешности
, однако по мере уменьшения погрешности 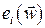 первое слагаемое в (3.10) начинает играть все более важную роль. Эффективность метода сильно зависит от выбора ut. Существуют различные способы подбора этого параметра, однако наиболее известна методика Д. Марквардта:
первое слагаемое в (3.10) начинает играть все более важную роль. Эффективность метода сильно зависит от выбора ut. Существуют различные способы подбора этого параметра, однако наиболее известна методика Д. Марквардта:
– если  , то
, то  , где r >1 – коэффициент уменьшения u;
, где r >1 – коэффициент уменьшения u;
– если 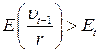 , а
, а 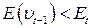 , то
, то 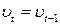 ;
;
– если 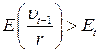 и
и  , то
, то  до достижения
до достижения  .
.
Заметим, что в непосредственной близости к точке решения u =0, процесс определения  сводится к аппроксимации 1–го порядка, а АЛМ превращается в алгоритм Гаусса–Ньютона, характеризующийся квадратичной сходимостью к оптимальному решению.
сводится к аппроксимации 1–го порядка, а АЛМ превращается в алгоритм Гаусса–Ньютона, характеризующийся квадратичной сходимостью к оптимальному решению.






