Такие уравнения имеют вид 
и 
, где 
- действительные числа, а функция f(x) непрерывна на интервале интегрирования X.
Сформулируем две теоремы, которые показывают, в каком виде искать общие решения ЛОДУ и ЛНДУ n-ого порядка.
Теорема.
Общим решением y0 линейного однородного дифференциального уравнения 
на интервале X с непрерывными коэффициентами 
на X является линейная комбинация nлинейно независимых частных решений ЛОДУ 
с произвольными постоянными коэффициентами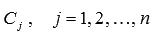 
, то есть 
.
Теорема.
Общее решение y линейного неоднородного дифференциального уравнения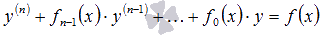 
на интервале X с непрерывными на том же промежутке X коэффициентами и функцией f(x)представляет собой сумму 
, где y0 - общее решение соответствующего ЛОДУ , а 
- какое-нибудь частное решение исходного ЛНДУ.
Таким образом, общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами ищем в виде , где - какое-нибудь его частное решение, а – общее решение соответствующего однородного дифференциального уравнения .
Сначала разберемся как находить - общее решение ЛОДУ n-ого порядка с постоянными коэффициентами, а в конце статьи покажем как определить частное решение линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами.
Алгебраическое уравнение n-ого порядка 
называетсяхарактеристическим уравнением линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами вида . Если мы найдем все n корней характеристического уравнения 
, то, исходя из их значений, можно определить n частных линейно независимых решений 
исходного ЛОДУ.
Перечислим все возможные варианты и разберем примеры на каждый из них.
1. Если все решения характеристического уравнения действительные и различные, то линейно независимые частные решения имеют вид
а общее решение ЛОДУ n-ого порядка с постоянными коэффициентами записывается как
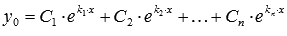
Пример.
Найдите общее решение линейного однородного дифференциального уравнения третьего порядка с постоянными коэффициентами 
.
Решение.
Запишем характеристическое уравнение и найдем его корни, предварительно разложив многочлен в левой части равенства на множители способом группировки:
Все три корня характеристического уравнения действительные и различные, поэтому общее решение ЛОДУ третьего порядка с постоянными коэффициентами имеет вид
.
2. Если все решения характеристического уравнения действительные и одинаковые, то есть, 
, то линейно независимые частные решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами имеют вид
а общее решение ЛОДУ имеет вид
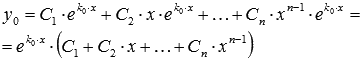
Пример.
Найдите общее решение дифференциального уравнения 
.
Решение.
Характеристическое уравнение этого ЛОДУ четвертого порядка имеет вид 
.
Если обратиться к формуле бинома Ньютона, то характеристическое уравнение можно переписать в виде 
, откуда виден его четырехкратный корень k0 = 2.
Таким образом, общее решение исходного линейного однородного дифференциального уравнения с постоянными коэффициентами есть
.
3. Если решениями характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами являются различные комплексно сопряженные пары 
, n=2m, то линейно независимые частные решения такого ЛОДУ имеют вид
а общее решение записывается как
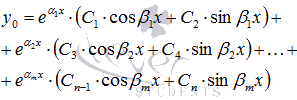
Пример.
Проинтегрируйте линейное однородное дифференциальное уравнение четвертого порядка с постоянными коэффициентами 
.
Решение.
Характеристическим уравнением данного ЛОДУ является 
. После проведения несложных преобразований и группировки получаем
Отсюда легко найти две пары комплексно сопряженных корней характеристического уравнения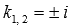 
и 
. Следовательно, общее решение исходного линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами имеет вид
4. Если решениями характеристического уравнения являются совпадающие комплексно сопряженные пары 
, то линейно независимые частные решения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами имеют вид
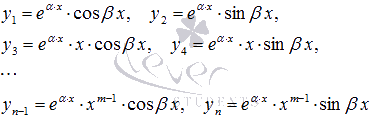
а общее решение такого ЛОДУ есть
Пример.
Найдите общее решение ЛОДУ с постоянными коэффициентами 
.
Решение.
Запишем характеристическое уравнение данного линейного однородного дифференциального уравнения с постоянными коэффициентами и найдем его корни:
То есть, решением характеристического уравнения является двукратная комплексно сопряженная пара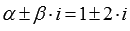 
. Поэтому общим решеним исходного линейного однородного дифференциального уравнения с постоянными коэффициентами является
.
5. Возможны любые комбинации предыдущих случаев, то есть, часть корней характеристического уравнения линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами действительные и различные, часть действительные и совпадающие, часть различных комплексно сопряженных пар и часть совпадающих комплексно сопряженных пар.
Пример.
Найдите общее решение дифференциального уравнения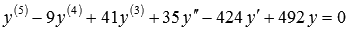 
.
Решение.
Характеристическое уравнение данного линейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид 
.
Многочлен в левой части равенства можно разложить на множители (смотрите раздел разложение многочлена на множители). Среди делителей свободного члена находим двукратный корень k1=k2=2 и корень k3=-3. Используя схему Горнера, приходим к разложению 
.
Из квадратного уравнения 
находим оставшиеся корни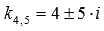 
.
Таким образом, общее решение исходного линейного однородного дифференциального уравнения с постоянными коэффициентами имеет вид
Итак, мы разобрали основные случаи, при которых можно найти y0 - общее решение ЛОДУ n-ого порядка с постоянными коэффициентами.
Теперь переходим к нахождению общего решения линейных неоднородных дифференциальных уравнений n-ого порядка с постоянными коэффициентами вида .
Их общее решение представляется в виде суммы общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ, то есть, как . Так как мы научились находить y0, то осталось научиться определять - частное решение линейного неоднородного дифференциального уравнения порядка n с постоянными коэффициентами.
Перечислим методы нахождения в зависимости от вида функции f(x), которая находится в правой части рассматриваемого ЛНДУ.
1. Если f(x) является многочленом n-ой степени f(x) = Pn(x), то частное решение ЛНДУ ищется в виде 
, где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю.
2. Если функция f(x) представлена произведением многочлена степени n и экспоненты 
, то частное решение ЛНДУ второго порядка ищется в виде 
, где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных 
.
3. Если функция f(x) имеет вид 
, где А1 и В1 – числа, то частное решение ЛНДУ представляется как 
, где А и В– неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных 
.
Рассмотрим линейное дифференциальное уравнение вида
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
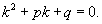Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
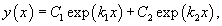где C1 и C2 − произвольные действительные числа.
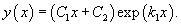
Рассмотренные три случая удобно представить в виде таблицы:
| |
| Пример 1 | |
Решить дифференциальное уравнение y'' − 6y' + 5y = 0.
Решение.
Запишем сначала соответствующее характеристическое уравнение:
Корни данного уравнения равны k1 = 1, k2 = 5. Поскольку корни действительны и различны, общее решение будет иметь вид:
где C1 и C2 − произвольные постоянные.
| |
| Пример 2 | |
Найти общее решение дифференциального уравнения y'' − 6y' + 9y = 0.
Решение.
Вычислим корни характеристического уравнения:
Как видно, характеристическое уравнение имеет один корень второго порядка: k1 = 3. Поэтому общее решение дифференциального уравнения определяется формулой
где C1, C2 − произвольные действительные числа.
| |
| Пример 3 | |
Решить дифференциальное уравнение y'' − 4y' + 5y = 0.
Решение.
Сначала запишем соответствующее характеристическое уравнение и определим его корни:
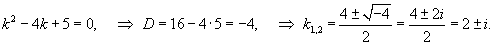Таким образом, характеристическое уравнение имеет пару комплексно-сопряженных корней: k1 = 2 + i,k2 = 2 − i. В этом случае общее решение выражается формулой
где C1, C2 − произвольные постоянные.
| |
| Пример 4 | |
Решить уравнение y'' + 25y = 0.
Решение.
Характеристическое уравнение имеет вид:
Корни этого уравнения являются чисто мнимыми:
Тогда ответ записывается в следующем виде:
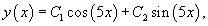где C1, C2 − постоянные интегрирования.
| |
| Пример 5 | |
Решить уравнение y'' + 4iy = 0.
Решение.
В данном уравнении коэффициент перед y является комплексным числом. Общее решение линейного дифференциального уравнения с постоянными комплексными коэффициентами конструируется так же, как и в случае действительных коэффициентов. Сначала запишем характеристическое уравнение:
Определим корни уравнения:
Вычислим отдельно квадратный корень из мнимой единицы. Для этого число i удобно представить в тригонометрической форме:
Корни характеристического уравнения будут равны:
Общее решение исходного дифференциального уравнения будет выражаться линейной комбинацией следующих экспоненциальных функций:
где C1, C2 − произвольные постоянные.
39.Основные понятия комбинаторики.
Комбинато́рика— раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов.
Число всех перестановок порядка n равно факториалу: Pn=n!
Факториа́лчисла n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно.
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
1! = 1,
2! = 2•1 = 2,
3! = 3 •2 •1 = 6,
4! = 4 •3 •2 •1 = 24,
Задача.Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно положить любой из четырех шариков, на второе – любой из трех оставшихся, на третье – любой из двух оставшихся, а на четвертое – последний оставшийся шарик. Итак, ответ: 4 • 3 • 2 • 1 = 4!.
Задача. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?
Решение. Перечислим все возможные варианты:
20 22 26
30 32 36
60 62 66
70 72 76
90 92 96
Вопрос 40. Определение вероятности. Основные понятия.
Явление, действие или эксперимент будем называть испытанием. Результат такого испытания будем называть событием или исходом.
Вероятность какого либо события обозначается P. P(A)-вероятность наступления события А.
Событие называется достоверным, если оно происходит в результате некоторого испытания. Обозначается V=1. V-считается невозможным, если оно некогда не наступает в результате некоторого испытания.
Вероятность какого либо события 0≤P(A)≤1
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
P(A)= 
Вопрос 41. Основные определение теории множеств. Диаграммы Эйлера-Венна.
Под множеством принято понимать совокупность объединенных по общим признакам различных предметов. Множества будем обозначать прописными латинскими буквами A, B,C, …, X, Y, Z, а элементы, принадлежащие данным множествам – строчными a, b, c, …, x, y, z. Если a есть элемент множества A, то пишут  . Если a не является элементом множества A, пишут  . Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ. Рассматриваемое исходное множество называется универсальным и обозначаются U. Если все элементы множества A являются также элементами множества B, то говорят, что А включается в B или A является подмножеством множества B и обозначается  . Если 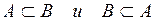 , то говорят, что A=B или A совпадает с B.
|
Диаграмами Ейлера-Вена называються фигури, с помощью которых изобрахают на плоскости множества и наглядно демонстрируют свойства операций над множествами. Прямоугольник на плоскости означает некоторое универсальное множество, которое включает в себя рассматриваемые множества.
Диграма Ейлера- Вена
Объединением двух множеств A и B называется множество, составленное из элементов, входящих хотя бы в одно из данных множеств, оно обозначается 
. Соответствующая диаграмма Ейлера- Вена:
Объединением некоторой совокупности множеств 
называется множество S, составленное из всех элементов, входящих хотя бы в одно из слагаемых множеств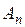 
, и обозначаемое 
.
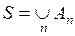Пересечением двух множеств A и B называется множество, составленное из всех элементов, принадлежащих как множеству A, так и множеству B, и обозначается 
. Соответствующая диаграмма Ейлера- Вена:
рямым (или декартовым) произведением двух множеств A и B называется множество всевозможных пар (x, y), где 
. Произведение множеств A и B обознначается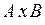 
.
Дополнением к множеству A называется множество 
, состоящее из элементов универсального множества, U не принадлежащих множеству A, т.е.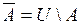 
.
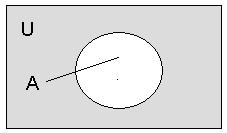
Рисунок5. Дополнение к множеству A
Операции над множествами имеют следующие свойства:
1. Коммутативность: 
.
2. Ассоциативность: 
.
3. Дистрибутивность: 
.
4. Законы де Моргана: 
.
Определения теории графов. Планарность. Построение плоских укладок графа.
