Чтобы вычислить определитель матрицы  второго порядка, надо от произведения элементов главной диагоналиотнять произведение элементов побочной диагонали:
второго порядка, надо от произведения элементов главной диагоналиотнять произведение элементов побочной диагонали:

Пример
Задание. Вычислить определитель второго порядка 
Решение. 
Ответ. 
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:

Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком "плюс"; аналогично, для второго определителя - соответствующие произведения берутся со знаком "минус", т.е.

Пример
Задание. Вычислить определитель  методом треугольников.
методом треугольников.
Решение. 

Ответ. 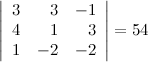
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":


Пример
Задание. Вычислить определитель  с помощью правила Саррюса.
с помощью правила Саррюса.
Решение. 

Ответ. 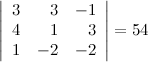
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель 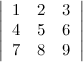
Решение. 
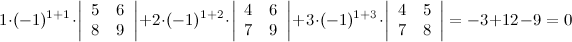
Ответ. 
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель 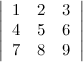
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.

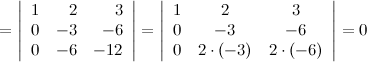
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. 
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель  , разложив его по элементам какой-то строки или какого-то столбца.
, разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй - пять третьих и от четвертой - три третьих строки, получаем:
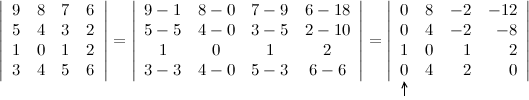
Полученный определитель разложим по элементам первого столбца:

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей - вторую:

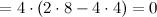
Ответ. 
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Теорема Лапласа
Теорема
Пусть 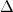 - определитель
- определитель  -го порядка. Выберем в нем произвольные
-го порядка. Выберем в нем произвольные  строк (или столбцов), причем
строк (или столбцов), причем  . Тогда сумма произведений всех миноров
. Тогда сумма произведений всех миноров  -го порядка, которые содержатся в выбранных
-го порядка, которые содержатся в выбранных  строках (столбцах), на их алгебраические дополнения равна определителю.
строках (столбцах), на их алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель 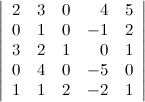
Решение. Выберем в данном определителе пятого порядка две строки - вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):



Ответ. 
8 Системой m линейных уравнений с n неизвестными называется система вида

где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы  , которую назовём матрицей системы.
, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. - И третий случай, когда система вообще не имеет решения. Например,
 , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы  и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов 
Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
 или короче A∙X=B.
или короче A∙X=B.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A:  . Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
. Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A-1B.
Метод Крамера
Данный метод так же, как и матричный, применим только для систем линейных уравнений, у которых число неизвестных совпадает с числом уравнений. Метод Крамера основан на одноимённой теореме:
Теорема 5.2. Система  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными

основная матрица которой невырожденная, имеет единственное решение, которое может быть получено по формулам

где 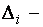 определитель матрицы, полученной из основной матрицы
определитель матрицы, полученной из основной матрицы  системы уравнений заменой её
системы уравнений заменой её  го столбца столбцом свободных членов.
го столбца столбцом свободных членов.
Пример. Найдём решение системы линейных уравнений, рассмотренной в предыдущем примере, методом Крамера. Основная матрица системы уравнений невырожденная, поскольку  Вычислим определители
Вычислим определители 



По формулам, представленным в теореме 5.2, вычислим значения неизвестных: 
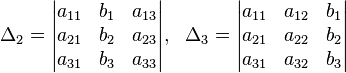
11. Метод Гаусса
Рассмотрим систему линейных уравнений  Метод Гаусса решения систем линейных уравнений состоит из двух этапов, называемых прямым и обратным ходом. Прямой ход метода Гаусса заключается в том, что с помощью элементарных преобразований над расширенной матрицей система
Метод Гаусса решения систем линейных уравнений состоит из двух этапов, называемых прямым и обратным ходом. Прямой ход метода Гаусса заключается в том, что с помощью элементарных преобразований над расширенной матрицей система  приводится к «ступенчатому» виду.
приводится к «ступенчатому» виду.
Обратный ход метода Гаусса состоит в том, что, начиная с последнего уравнения ступенчатой системы, вычисляются неизвестные.
При реализации прямого хода метода Гаусса возможны следующие три случая.
1. В результате преобразований в системе уравнений будет получено уравнение вида  где
где  Ясно, что никакой набор действительных чисел этому уравнению удовлетворять не может, поэтому в таком случае система уравнений несовместна.
Ясно, что никакой набор действительных чисел этому уравнению удовлетворять не может, поэтому в таком случае система уравнений несовместна.
2. В результате преобразований получится ступенчатая система уравнений

в которой количество уравнений совпадает с количеством неизвестных.
В этом случае система уравнений является определённой.
В результате преобразований получится система уравнений ступенчатого вида, в которой количество неизвестных больше числа уравнений системы (  )
)

В этом случае те неизвестные, которые стоят на «ступеньках», называются главными неизвестными (  ), а другие неизвестные называются свободными (
), а другие неизвестные называются свободными (  ); система уравнений будет неопределённой. Тогда обратный ход метода Гаусса состоит в том, что начиная с последнего уравнения системы, главные неизвестные выражаются через свободные и составляется общее решение системы уравнений. Для того чтобы получить какое-либо частное решение системы, свободным неизвестным придают конкретные числовые значения, вычисляя тем самым главные неизвестные.
); система уравнений будет неопределённой. Тогда обратный ход метода Гаусса состоит в том, что начиная с последнего уравнения системы, главные неизвестные выражаются через свободные и составляется общее решение системы уравнений. Для того чтобы получить какое-либо частное решение системы, свободным неизвестным придают конкретные числовые значения, вычисляя тем самым главные неизвестные.
Пример. Решить систему линейных уравнений методом Гаусса.

Прямой ход. Приведём расширенную матрицу системы

с помощью элементарных преобразований к ступенчатому виду. Переставим первую и вторую строки матрицы  , получим матрицу
, получим матрицу

Сложим вторую строку полученной матрицы с первой, умноженной на  а её третью строку – с первой строкой, умноженной на
а её третью строку – с первой строкой, умноженной на 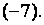 Получим матрицу
Получим матрицу
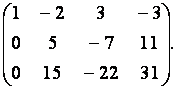
К третьей строке полученной матрицы прибавим вторую строку, умноженную на  в результате чего получим ступенчатую матрицу
в результате чего получим ступенчатую матрицу

Таким образом, мы привели данную систему уравнений к ступенчатому виду:
 ,
,
Обратный ход. Начиная с последнего уравнения полученной ступенчатой системы уравнений, последовательно найдём значения неизвестных: 
Однородная система линейных уравнений всегда совместна: она имеет хотя бы одно решение – нулевое (так называемое, тривиальное решение). Нас будут интересовать только нетривиальные решения однородной системы линейных уравнений. Рассмотрим пример решения однородной системы линейных уравнений методом Гаусса.
Пример. Решить систему линейных уравнений методом Гаусса.

Прямой ход. Поскольку данная система уравнений является однородной, выясним, имеет ли эта система нетривиальные решения.
Для этого вычислим определитель основной матрицы системы

Вычисляя определитель  разложением по строке или по столбцу, получим
разложением по строке или по столбцу, получим 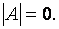 В соответствии с теоремой 5.1, данная система линейных уравнений имеет нетривиальное решение. Приведём основную матрицу к ступенчатому виду с помощью элементарных преобразований. Сложим вторую и четвёртую строки матрицы
В соответствии с теоремой 5.1, данная система линейных уравнений имеет нетривиальное решение. Приведём основную матрицу к ступенчатому виду с помощью элементарных преобразований. Сложим вторую и четвёртую строки матрицы  с первой строкой, умноженной на
с первой строкой, умноженной на  а третью строку – с первой строкой, умноженной на
а третью строку – с первой строкой, умноженной на  получим матрицу
получим матрицу

Сложим третью строку полученной матрицы со второй, умноженной на  а четвёртую строку – с третьей строкой; получим матрицу
а четвёртую строку – с третьей строкой; получим матрицу

В этой матрице удалим нулевые строки и получим ступенчатую матрицу

Тем самым, данная система приведена к ступенчатому виду:

Неизвестные  и
и  стоящие на «ступеньках», являются главными, а неизвестные
стоящие на «ступеньках», являются главными, а неизвестные  и
и  свободными.
свободными.
Обратный ход. Выразим из второго уравнения системы главную неизвестную 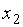 через свободные неизвестные
через свободные неизвестные  и
и 
 Используя полученное равенство, из первого уравнения ступенчатой системы получим следующее выражение главной неизвестной
Используя полученное равенство, из первого уравнения ступенчатой системы получим следующее выражение главной неизвестной 
 Общее решение данной системы уравнений запишем в виде:
Общее решение данной системы уравнений запишем в виде: 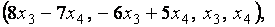 где
где  и
и  любые действительные числа. Положив, к примеру,
любые действительные числа. Положив, к примеру, 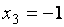 и
и  получим частное решение системы:
получим частное решение системы: 
Ко́мпле́ксные чи́сла — числа вида  , где
, где  и
и  — вещественные числа,
— вещественные числа,  — мнимая единица (величина, для которой выполняется равенство:
— мнимая единица (величина, для которой выполняется равенство:  ). Множество всех комплексных чисел с арифметическими операциями является полем и обычно обозначается
). Множество всех комплексных чисел с арифметическими операциями является полем и обычно обозначается  отлат. complex — тесно связанный.
отлат. complex — тесно связанный.
Геометрическая интерпретация комплексного числа
Комплексные числа можно изображать на комплексной плоскости следующим образом: действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.
Любое комплексное число  можно изобразить как точку на комплексной плоскости с координатами
можно изобразить как точку на комплексной плоскости с координатами  и
и  , где ось абсцисс называется вещественной, а ось ординат — мнимой.
, где ось абсцисс называется вещественной, а ось ординат — мнимой.
Определение 1:
Модулем комплексного числа называется корень суммы квадратов его действительной и мнимой частей. 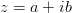 ,
, 
 ,
,


Определение 2:
Величина угла, который образует вектор изображающий данное число на комплексной плоскости с вещественной осью называется аргументом этого комплексного числа 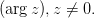
Угол, отсчитываемый от оси против часовой стрелки — отрицательный, по — положительный.
Углы, отличающиеся на  , соответствуют одному и тому же числу и записываются как:
, соответствуют одному и тому же числу и записываются как:
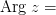
 ,
,  .
.
Определение 3:
У комплексного числа существует тригонометрическая форма записи 

13. Операции над комплексными числами,заданными в алгебраической форме,Примеры
Действия над комплексными числами, записанными в алгебраической форме
Алгебраической формой комплексного числа z = (a, b).называется алгебраическое выражение вида
z = a + bi.
(это мнимая 1(еденица),число которое в квадрате(2 степени) дает число -1(минус один))
Арифметические операции над комплексными числами z1 = a1 + b1i и z2 = a2 + b2i, записанными в алгебраической форме, осуществляются следующим образом.
1. Сумма (разность) комплексных чисел
z1 ± z2 = (a1 ± a2) + (b1±b2)∙i,
т.е. сложение (вычитание) осуществляются по правилу сложения многочленов с приведением подобных членов.
2. Произведение комплексных чисел
z1∙z2 = (a1∙a2 - b1∙b2) + (a1∙b2 + a2∙b1)∙i,
т.е. умножение производится по обычному правилу умножения многочленов, с учетом того, что i2=1.
3. Деление двух комплексных чисел осуществляется по следующему правилу:
 , (z2 ≠ 0),
, (z2 ≠ 0),
т.е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.
Возведение в степень комплексных чисел определяется следующим образом:
 .
.
Легко показать, что

Примеры.
1. Найти сумму комплексных чисел z1 = 2 – i и z2 = –4 + 3i.
z1 + z2 = (2 + (–1)∙i)+ (–4 + 3i) = (2 + (–4)) + ((–1) + 3) i = –2+2i.
2. Найти произведение комплексных чисел z1 = 2 – 3i и z2 = –4 + 5i.
gif" name="object72" align=bottom width=41 height=21> = (2 – 3i) ∙ (–4 + 5i) = 2 ∙(–4) + (-4) ∙(–3i) + 2∙5i – 3i∙5i =7+22i.
3. Найти частное z от деления z1 = 3 – 2 на z2 = 3 – i.
z = 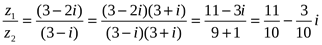 .
.
4. Решить уравнение: 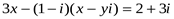 , x и y Î R.
, x и y Î R.

(2x + y) + (x + y)i = 2 + 3i.
В силу равенства комплексных чисел имеем:

откуда x = –1, y = 4.
5. Вычислить: i2, i3, i4, i5, i6, i-1, i-2.
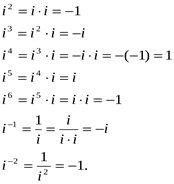
6. Вычислить  , если
, если  .
.

 .
.
7. Вычислить число  обратное числу z =3-i.
обратное числу z =3-i.
 .
.
14. Триганометрическая форма комплексного числа,Формула Муавра,Примеры.
комплексные числа в тригонометрической форме
Комплексной плоскостью называется плоскость с декартовыми координатами (x, y), если каждой точке с координатами (a, b) поставлено в соответствие комплексное число z = a + bi. При этом ось абсцисс называется действительной осью, а ось ординат – мнимой. Тогда каждое комплексное число a + bi геометрически изображается на плоскости как точка A (a, b) или вектор  .
.
Следовательно, положение точки А (и, значит, комплексного числа z) можно задать длиной вектора |  | = r и углом j, образованным вектором |
| = r и углом j, образованным вектором |  | с положительным направлением действительной оси. Длина вектора называется модулем комплексного числа и обозначается | z |=r, а угол j называется аргументом комплексного числа и обозначается j = arg z.
| с положительным направлением действительной оси. Длина вектора называется модулем комплексного числа и обозначается | z |=r, а угол j называется аргументом комплексного числа и обозначается j = arg z.
Ясно, что | z | ³ 0 и | z | = 0 Û z = 0.
Из рис. 2 видно, что  .
.
Аргумент комплексного числа определяется неоднозначно, а с точностью до 2pk, k Î Z.
Из рис. 2 видно также, что если z=a+bi и j=arg z, то
cosj =  , sinj =
, sinj =  , tgj =
, tgj =  .
.
Если zÎ R и z > 0, то arg z = 0 +2pk;
если z Î R и z < 0, то arg z = p + 2pk;
если z = 0, arg z не определен.
Главное значение аргумента определяется на отрезке 0 £ arg z £ 2p,
либо -p £ arg z £ p.
Примеры:
1. Найти модуль комплексных чисел z1 = 4 – 3i и z2 = –2–2i.
 ;
;
 .
.
2. Определить на комплексной плоскости области, задаваемые условиями:
1) | z | = 5; 2) | z | £ 6; 3) | z – (2+i) | £ 3; 4) 6 £ | z – i | £ 7.
Решения и ответы:
1) | z | = 5 Û  Û
Û  - уравнение окружности радиусом 5 и с центром в начале координат.
- уравнение окружности радиусом 5 и с центром в начале координат.
2) Круг радиусом 6 с центром в начале координат.
3) Круг радиусом 3 с центром в точке z0 = 2 + i.
4) Кольцо, ограниченное окружностями с радиусами 6 и 7 с центром в точке z0 = i.
3. Найти модуль и аргумент чисел: 1)  ; 2)
; 2) 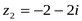 .
.
1)  ; а = 1, b =
; а = 1, b = 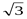 Þ
Þ  ,
,
 Þ j1 =
Þ j1 =  .
.
2) z2 = –2 – 2i; a = –2, b = -2 Þ  ,
,
 .
.
Указание: при определении главного аргумента воспользуйтесь комплексной плоскостью.
Используя формулы  можно перейти от алгебраической формы записи комплексных чисел к тригонометрической форме (формула Муавра):
можно перейти от алгебраической формы записи комплексных чисел к тригонометрической форме (формула Муавра):
 .
.
Комплексные числа в тригонометрической форме равны тогда и только тогда, когда равны их модули, а аргументы отличаются на целое число кратное 2p.
4. Записать числа в тригонометрической форме.
1) 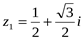 , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  .
.
1) 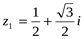 ,
, 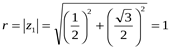 ,
,
 .
.
(За значение угла берем наименьшее неотрицательное из возможных значений аргумента.)
Таким образом: z1 = 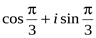 .
.
2) 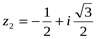 , r2 = 1, j2 =
, r2 = 1, j2 =  ,
,  .
.
3)  , r3 = 1, j3 =
, r3 = 1, j3 = 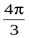 ,
,  .
.
4)  , r4 = 1, j4 =
, r4 = 1, j4 = 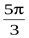 ,
,  .
.
Действия над комплексными числами, заданными в тригонометрической форме
1. Умножение.
При перемножении чисел z1 и z2, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
z = z1z2 = r1r2×(cos(j1 + j2) + isin(j1 + j2)).
(Формула справедлива для любого конечного числа сомножителей.)
z1…zn = r1…rn (cos(j1 +…+jn) + isin(j1 +…+jn)).
Если z1 = z2 =…= zn = z = r(cosj + isinj), то последняя принимает вид
zn = rn×(cosnj + isin nj)
и называется формулой Муавра. Она показывает, что для возведения комплексного числа в натуральную степень нужно возвести в эту степень его модуль, а аргумент умножить на показатель степени.
Примеры.
1) Выполнить умножение: 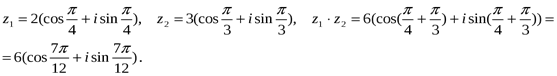
2) Вычислить:  .
.

2. Деление.
Если z1 = r1×(cosj1 + isinj1) и z2 = r2×(cosj2 + isinj2), то
 ,
,
т.е. модуль частного двух комплексных чисел z1 и z2 равен частному модулей, а аргумент частного – разности аргументов.
Пример.
z1 =  z2 =
z2 =  . Найти частное.
. Найти частное.
 .
.
Формула Муавра ( ) находит много применений. Так, например, если n = 3, то, возведя левую часть по формуле сокращенного умножения в куб, получим равенство
) находит много применений. Так, например, если n = 3, то, возведя левую часть по формуле сокращенного умножения в куб, получим равенство
 .
.
Из равенства комплексных чисел и основного тригонометрического тождества получаем

15. Показательныя форма комплексного числа,Основыне операции
Показательная форма комплексного числа
Формула Эйлера
Пусть  - некоторое комплексное число. По определению полагают, что
- некоторое комплексное число. По определению полагают, что
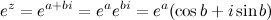
Если число  - действительное, то есть
- действительное, то есть  , то
, то

Если число  - чисто мнимое, то есть
- чисто мнимое, то есть  , то
, то

Таким образом, имеем равенство

которое называется формулой Эйлера.
Показательная форма записи комплексного числа
Рассмотрим произвольное комплексное число, записанное в тригонометрической форме:  . По формуле Эйлера
. По формуле Эйлера

а тогда

Следовательно, любое комплексное число можно представить в так называемой показательной форме:

Операции с комплексными числами в показательной форме
Такая форма представления позволяет дать наглядную интерпретацию операциям умножения комплексных чисел, их деления и возведения комплексного числа в степень. Например, умножение комплексного числа 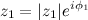 на комплексное число
на комплексное число 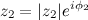 выглядит следующим образом:
выглядит следующим образом:
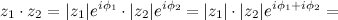

То есть, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.
Аналогично можно довольно легко найти частное от деления комплексного числа 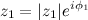 на комплексное число
на комплексное число 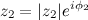 :
:

Отсюда получаем правило, что для того чтобы найти частное двух комплексных чисел, надо поделить их модули и отнять аргументы.
Для возведения комплексного числа  в целую степень
в целую степень  нужно представить это число в показательной форме
нужно представить это число в показательной форме  , модуль возвести в степень, а аргумент увеличить в
, модуль возвести в степень, а аргумент увеличить в  раз:
раз:

16. Предел функции,Свойства пределов.
Предел функции в точке и на бесконечности
Пусть  - функция с областью определения
- функция с областью определения  , причем
, причем  - некоторое число.
- некоторое число.
Число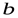 называется пределом функции
называется пределом функции  в предельной точке
в предельной точке  , если значения функции неограниченно приближаются к числу
, если значения функции неограниченно приближаются к числу 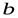 , при всех значениях
, при всех значениях  , достаточно близких к
, достаточно близких к 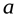 . Предел функции в точке
. Предел функции в точке  обозначается
обозначается  .
.
Предел  называется пределом слева данной функции в точке
называется пределом слева данной функции в точке  .
.
Предел  называется пределом справа данной функции.
называется пределом справа данной функции.

Если область определения  функции
функции  содержит сколь угодно большие по абсолютной величине положительные (отрицательные) значения gif" name="object20" align=absmiddle width=18 height=18>, то в этом случае можно рассматривать предел функции на бесконечности.
содержит сколь угодно большие по абсолютной величине положительные (отрицательные) значения gif" name="object20" align=absmiddle width=18 height=18>, то в этом случае можно рассматривать предел функции на бесконечности.
Число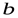 называется пределом функции
называется пределом функции  при
при  , если аргумент
, если аргумент  , изменяясь, принимает сколь угодно большие по абсолютной величине значения
, изменяясь, принимает сколь угодно большие по абсолютной величине значения  , а соответствующая последовательность значений функции сходится (приближается) к числу
, а соответствующая последовательность значений функции сходится (приближается) к числу 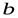 :
:  .
.

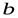


Предел функции при
при  равен
равен  , если для любой сходящейся к
, если для любой сходящейся к  последовательности значений аргумента соответствующая последовательность значений функции неограниченно возрастает:
последовательности значений аргумента соответствующая последовательность значений функции неограниченно возрастает:  .
.
Пример 1.  .
.

2. Основные свойства пределов
Все свойства имеют смысл, если пределы функций существуют.
1. Если предел функции в точке 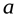 существует, то он единственный.
существует, то он единственный.
2. Предел постоянной величины равен самой постоянной:
 .
.
3. Предел суммы (разности) конечного числа функций равен соответственно сумме (разности) пределов этих функций:
 .
.
4. Предел произведения конечного числа функций равен произведению пределов этих функций:
 .
.
Следствие. Постоянный множитель можно выносить за знак предела:
 .
.
5. Предел частного двух функций равен частному пределов этих функций:
 (если
(если  ).
).
Если предельная точка  принадлежит области определения элементарной функции
принадлежит области определения элементарной функции 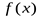 , то вычисление предела
, то вычисление предела  сводится к подстановке в функцию вместо
сводится к подстановке в функцию вместо  числа
числа  , вычислению значения
, вычислению значения  и записи
и записи  .
.
Пример 2. Вычислить пределы.
1)  . Точка
. Точка  принадлежит области определения функции
принадлежит области определения функции  , значит,
, значит,  .
.
2)  =
=  .
.
3. Бесконечно малые и бесконечно большие функции
Функция называется бесконечно малой функцией при
называется бесконечно малой функцией при  , если
, если 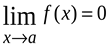 .
.
Пример 3.
Функция  - б.м.ф. в точках
- б.м.ф. в точках  , т.к.
, т.к.  .
.
Функция  - б.м.ф. при
- б.м.ф. при  , т.к.
, т.к. 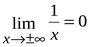 .
.
Функция называется бесконечно большой функцией при
называется бесконечно большой функцией при  , если
, если 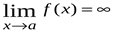 .
.
Пример 4. Функция - б.б.ф. при
- б.б.ф. при  , т.к.
, т.к.  .
.
Теорема (Свойства б.м.ф.)
Алгебраическая сумма конечного числа б.м.ф. и произведение конечного числа б.м.ф. есть бесконечно малая функция.
Произведение б.м.ф. на ограниченную функцию есть бесконечно малая функция.
Частное от деления б.м.ф. на функцию, имеющую в точке ненулевой предел, есть б.м.ф.
ненулевой предел, есть б.м.ф.
Функция, обратная к бесконечно малой, есть бесконечно большая функция.
Теорема (Свойства б.б.ф.)
Произведение конечного числа б.б.ф. есть бесконечно большая функция.
Произведение б.б.ф. на функцию, имеющую предел, не равный нулю, есть бесконечно большая функция.
Функция, обратная к бесконечно большой, есть бесконечно малая функция.
17. Непрерывность фунции.Основные определения
Непрерывность функций
Определение непрерывности функции
Функция 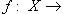
 , называется непрерывной в точке
, называется непрерывной в точке  , если выполняется одно из эквивалентных условий:
, если выполняется одно из эквивалентных условий:
1) 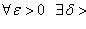
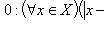

 ; (1)
; (1)
2) для произвольной последовательности (xn) значений  , сходящейся при n → ∞ к точке x0, соответствующая последовательность (f(xn)) значений функции сходится при n → ∞ к f(x0);
, сходящейся при n → ∞ к точке x0, соответствующая последовательность (f(xn)) значений функции сходится при n → ∞ к f(x0);
3) 
 или f(x) - f(x0) → 0 при x - x0 → 0;
или f(x) - f(x0) → 0 при x - x0 → 0;
4) 
 такое, что
такое, что



или, что то же самое,
f: ]x0 - δ, x0 + δ[ → ]f(x0) - ε, f(x0) + ε[.
Из определения непрерывности функции f в точке x0 следует, что
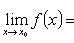

Если функция f непрерывна в каждой точке интервала ]a, b[, то функция f называется непрерывной на этом интервале.
Функция f: ]a, x0] → R (f: [x0, b[ → R) называется непрерывной в точке x0 слева (справа), если выполняется одно из эквивалентных условий:
1) 
 такое, что неравенство (1) выполняется, как только x0 - δ < x ≤ x0 (x0 ≤ x < x0 + δ);
такое, что неравенство (1) выполняется, как только x0 - δ < x ≤ x0 (x0 ≤ x < x0 + δ);
2) для произвольной последовательности (xn) значений 
 , сходящейся к точке x0, соответствующая последовательность (f(xn)) значений функции f сходится к f(x0);
, сходящейся к точке x0, соответствующая последовательность (f(xn)) значений функции f сходится к f(x0);
3) 

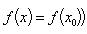 или, короче, если f(x0 - 0) = f(x0) (f(x0 + 0) = f(x0));
или, короче, если f(x0 - 0) = f(x0) (f(x0 + 0) = f(x0));
4) 
 такое, что
такое, что





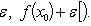
Функция f: X → R непрерывна во внутренней точке  тогда и только тогда, когда она в этой точке непрерывна слева и справа.
тогда и только тогда, когда она в этой точке непрерывна слева и справа.
Теорема 1. Если функция 
 , непрерывна в точке
, непрерывна в точке  , а функция f: X → R непрерывна в точке
, а функция f: X → R непрерывна в точке  , где x0 = g(t0), то композиция f ◦ g: T → R непрерывна в точке t0.
, где x0 = g(t0), то композиция f ◦ g: T → R непрерывна в точке t0.
Теорема 2. Пусть функции f: X → R и g: X → R,  , непрерывны в точке
, непрерывны в точке  . Тогда функции
. Тогда функции
f + g, fg и f/g (g(x0) ≠ 0),
непрерывны в точке x0.
Все элементарные функции непрерывны в области существования.
Точки разрыва функции и их классификация. Особые точки функции
Если функция f: X → R не является непрерывной в точке x0 ϵ X, то говорят, что она терпит разрыв в этой точке. При этом точка x0 называется точкой разрыва функции f.
Точки разрыва функции f классифицируем следующим образом:
1. Пусть x0 ϵ X - точка разрыва функции f и существует  , конечный или бесконечный. При этом:
, конечный или бесконечный. При этом:
а) если  конечный, то x0 называем точкой устранимого разрыва функции f;
конечный, то x0 называем точкой устранимого разрыва функции f;
б) если  , то x0 называем точкой разрыва типа полюс.
, то x0 называем точкой разрыва типа полюс.
2. Если  не существует, то точку x0 ϵ X называем точкой существенного разрыва функции f. При этом
не существует, то точку x0 ϵ X называем точкой существенного разрыва функции f. При этом
а) если существуют конечные пределы
f(x0 - 0), f(x0 + 0) (f(x0 - 0) ≠ f(x0 + 0)),
то точку x0 называем точкой разрыва первого рода функции f;
б) все остальные точки существенного разрыва называем точками разрыва второго рода функции f.
Поскольку в изолированной точке x0 ϵ X функция f: X → R непрерывна, то ее точками разрыва могут быть лишь предельные точки x ϵ X.
Основные свойства непрерывных функций
Функция f: [a, b] → R называется непрерывной на сегменте [a, b], если она непрерывна на интервале ]a, b[ и в точке a непрерывна справа, а в точке b - слева.
Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], тогда:
1) она ограничена на этом сегменте;
2) если 

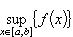 , то на сегменте [a, b] существуют точки x1 и x2 такие, что f(x1) = m, f(x2) = M (теорема Вейерштрасса);
, то на сегменте [a, b] существуют точки x1 и x2 такие, что f(x1) = m, f(x2) = M (теорема Вейерштрасса);
3) она принимает на каждом сегменте 
 , все промежуточные значения между f(α) и f(β) (теорема Коши).
, все промежуточные значения между f(α) и f(β) (теорема Коши).
В частности, если f(α)f(β) < 0, то найдется такое значение γ (α < γ < β), то f(γ) = 0.
Функция f: ]a, b[ → R называется кусочно-непрерывной на интервале ]a, b[, если она непрерывна во всех точках этого интервала, кроме конечного числа точек разрыва первого рода и конечного числа точек устранимого разрыва.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению еёаргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Таблица производных
| Производные степенных функций | Производные тригонометрических функций | Производные обратных тригонометрических функций |

| 
| 
|

| 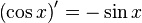
| 
|

| 
| 
|

| 
| 
|
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Свойства:
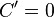
· 
·  [2]
[2]
·  [3]
[3]
· 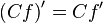
·






