Дифференциальные уравнения с разделяющимися переменными.
Среди обыкновенных дифференциальных уравнений первого порядка существуют такие, в которых возможно переменные x и y разнести по разные стороны знака равенства. В уравнениях вида 
переменные уже разделены, а в ОДУ 
переменные разделяются посредством преобразований. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.
В этой статье сначала рассмотрим метод решения уравнений с разделенными переменными, далее перейдем к уравнениям с разделяющимися переменными и закончим дифференциальными уравнениями, сводящимися к уравнениям с разделяющимися переменными. Для пояснения теории будем подробно разбирать решения характерных примеров и задач.
- Дифференциальные уравнения с разделенными переменными .
- Дифференциальные уравнения с разделяющимися переменными .
- Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными
, a ≠ 0, b ≠ 0. - Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными
или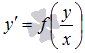 
. - Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными
.
Дифференциальные уравнения с разделенными переменными .
Дифференциальные уравнения называют уравнениями с разделенными переменными.
Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него.
Будем считать, что функции f(y) и g(x) непрерывны.
Общим интегралом уравнения с разделенными переменными является равенство 
. Если интегралы из этого равенства выражаются в элементарных функциях, то мы можем получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y) = 0, а иногда получается выразить функцию y в явном виде.
Пример.
Найдите общее решение дифференциального уравнения с разделенными переменными 
.
Решение.
Проинтегрируем обе части равенства: 
. По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их, используя таблицу первообразных:
где С1 и С2 – произвольные постоянные.
Мы пришли к неявно заданной функции 
, которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде. Но в нашем случае искомую функцию y можно выразить явно через аргумент x. Итак, 
, где 
. То есть, функция 
является общим решением исходного дифференциального уравнения.
Замечание.
Ответ можно записать в любом из трех видов или , или . Но имейте в виду, что многие преподаватели наряду с Вашим умением решать дифференциальные уравнения хотят также проверить умение брать интегралы и преобразовывать выражения. Так что, если есть возможность, старайтесь ответ давать в виде явной функции y или в виде неявно заданной функции Ф(x, y) = 0.
