Ідеальна структура системи. Для рішення завдання синтезу алгоритмічної структури повинні бути відомі передатна функція  об'єкта керування, збурювання
об'єкта керування, збурювання  й
й  діючі на вході й виході об'єкта, а також перешкода g виникаюча в каналах завдання й виміру.
діючі на вході й виході об'єкта, а також перешкода g виникаюча в каналах завдання й виміру.


У найпростішому випадку, що коли обурюють впливи на об'єкт відсутні, управління можна здійснювати за розімкнутою схемою (мал.2).
Якщо при цьому передатну функцію Wy(р) управляючого пристрою прийняти рівної
 , (1)
, (1)
те забезпечиться повна (структурна) компенсація інерційності об'єкта, і система керування буде практично миттєво відтворювати на виході об'єкта вплив, що задає, хопт(р). Завдання хопт(р) формується спеціальним фільтром з передатною функцією Фопт(р), що вибирається так, щоб фільтр якнайкраще про пускав всі складові сигналу х(p) і подавляв перешкоду g(p).
Якщо на об'єкт діє збурювання f(p)≠ 0 яке піддається виміру, то теоретично можна синтезувати ідеальну розімкнуту систему керування з повною компенсацією збурювання.
Причому, передатна функція (1), що забезпечує повну компенсацію інерційності об'єкта, виявляється найкращої й для компенсації збурювання f(p). Дійсно, при виконанні умови (1) завжди  , тому корисна складова yu(p) на виході об'єкта буде повністю врівноважувати збурювання f(p).
, тому корисна складова yu(p) на виході об'єкта буде повністю врівноважувати збурювання f(p).
Але збурювання f(p), як правило, не вдається виміряти, і систему керування доводиться будувати за замкнутою схемою або принципу зворотного зв'язку. Для відшукання структури ідеальної замкнутої системи можна використовувати ідею непрямого виміру збурювання f(p) за допомогою моделі об'єкта  .
.
Очевидно, що при  сигнал, що обчислюється на виході моделі
сигнал, що обчислюється на виході моделі
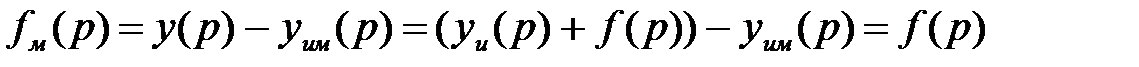
є побічно обмірюваним збурюванням f(p) і його можна, як і в попередній схемі ввести в керуючий пристрій з передатною функцією 1/Wo(р) і, таким чином, знову одержати ідеальну розімкнуту структуру. У ній відповідно до правил структурних перетворень сигнал yuм(p) можна перенести на вхід керуючого пристрою й прикласти до суматора 2. Тоді керуючий пристрій 1/Wo(р) виявиться охопленим внутрішнім позитивним зворотним зв'язком, а сигнал після суматора 1 буде відповідати сигналу помилки ε(p)=х(p)-y(p). Останнє означає, що система стала замкнутої й працює за принципом негативного зворотного зв'язку з регулятором - штрихової прямокутник:
 . (2)
. (2)
При точному збігу моделі й об'єкта регулятор (4) буде працювати як пропорційний з  , що відповідає нульовим помилкам по каналах завдання й збурювання.
, що відповідає нульовим помилкам по каналах завдання й збурювання.
У загальному випадку, коли f(p)≠ 0 і g(p)≠ 0 алгоритмічна структура ідеальної замкнутої системи сполучить у собі ознаки обох структур, обґрунтованих вище евристичним шляхом.
У цій ідеальній структурі регулятор також містить внутрішній позитивний зворотний зв'язок, ланки 1/Wo(р),  , і крім того, - оптимальний фільтр Фопт(р). Замкнута система з таким регулятором теоретично еквівалентна ідеальній розімкнутій системі керування по збурюванню f(p), що практично миттєво відтворює завдання x(p) і повністю компенсує збурювання f(p). Передатна функція регулятора ідеальної системи
, і крім того, - оптимальний фільтр Фопт(р). Замкнута система з таким регулятором теоретично еквівалентна ідеальній розімкнутій системі керування по збурюванню f(p), що практично миттєво відтворює завдання x(p) і повністю компенсує збурювання f(p). Передатна функція регулятора ідеальної системи
 . (3)
. (3)
Ланка Фопт(р) вхідне в прямий ланцюг регулятора, здійснює оптимальну фільтрацію зовнішніх впливів і виробляє оптимальне завдання хопт(p). Зворотна модель об'єкта 1/Wo(р) компенсує його инерционность, а пряма  прогнозує вплив керуючого впливу u(p) на керовану змінну y(p) (обчислює тридцятилітній yu(p) на виході об'єкта). Тому що сигнал yuм(p) з виходу прогнозуючої ланки надходить на вхід регулятора з позитивним знаком, те вся система після чергової зміни керуючого впливу виявляється як би розімкнутою. Внаслідок цього реальна замкнута система теоретично еквівалентна розімкнутій системі керування по збурюванню f(p).
прогнозує вплив керуючого впливу u(p) на керовану змінну y(p) (обчислює тридцятилітній yu(p) на виході об'єкта). Тому що сигнал yuм(p) з виходу прогнозуючої ланки надходить на вхід регулятора з позитивним знаком, те вся система після чергової зміни керуючого впливу виявляється як би розімкнутою. Внаслідок цього реальна замкнута система теоретично еквівалентна розімкнутій системі керування по збурюванню f(p).
Використовуване в ідеальній системі включення послідовно з об'єктом ланки у вигляді зворотної моделі об'єкта є принциповою основою структурного й параметричного синтезу систем керування, а сам прийом називається методом компенсації інерційності об'єкта.
У практичних завданнях синтезу найчастіше застосовується часткова (параметрична) компенсація - усунення впливу однієї - двох (звичайно самих більших) постійних часу об'єкта. Для цього послідовно з інерційним об'єктом
 , (4)
, (4)
де To1 > To2 > To3 >…>Ton, включають ланку, що форсує, першого-другого порядку з передатною функцією
 , (5)
, (5)
для якої постійні часу повинні бути рівними компенсуємим постійним часу об'єкта, тобто
 ;
; 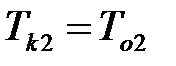 ,
,
і передатний коефіцієнт  .
.
Варто помітити, що практична реалізація систем з ідеальною структурою й застосування методу компенсації інерційності об'єкта пов'язані з певними технічними обмеженнями й перешкодами, які не завжди можуть бути переборені. Зокрема: як правило, неможливо точно реалізувати зворотну передатну функцію об'єкта (1); ланки, що форсують, виду (5), використовувані для часткової компенсації інерційності об'єкта, реально мають свою інерційність; регулятор із внутрішнім позитивним зворотним зв'язком звичайно структурно нестійкий або має великий передатний коефіцієнт, що викликає нереалізовані керуючі впливи. Проте, незважаючи на неможливість практичної реалізації системи з ідеальною структурою, вона є теоретичною межею, до якого необхідно прагнути при синтезуванні високоякісних систем керування. Відповідно до ідеальної структури можна сформулювати фундаментальний принцип структурно-параметричної оптимізації систем керування зі зворотним зв'язком:
керуючий пристрій повинен містити динамічну ланку з передатною функцією, рівної або близької зворотної передатної функції об'єкта.
Ідеальний регулятор для об'єктів із запізнюванням. Визначимо структуру й передатну функцію ідеального регулятора для інерційних об'єктів із запізнюванням, які можна описати наступною узагальненою передатною функцією
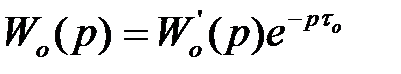 , (6)
, (6)
де  - дрібно-раціональна функція, що характеризує інерційну частину об'єкта,
- дрібно-раціональна функція, що характеризує інерційну частину об'єкта,  - чисте запізнювання об'єкта.
- чисте запізнювання об'єкта.
Урахуємо, що при підстановці передатної функції (6) у формулу (3) у передатній функції регулятора з'явиться співмножник  який відповідає ідеальному випереджувачу й точна реалізація якого технічно неможлива. Тому з метою спрощення шуканої структури регулятора й полегшення його технічної реалізації доцільно допустити, щоб для об'єктів, що містять чисте запізнювання
який відповідає ідеальному випереджувачу й точна реалізація якого технічно неможлива. Тому з метою спрощення шуканої структури регулятора й полегшення його технічної реалізації доцільно допустити, щоб для об'єктів, що містять чисте запізнювання  , ідеальна система відтворювала вплив, що задає, із
, ідеальна система відтворювала вплив, що задає, із  запізнюванням тобто Щоб
запізнюванням тобто Щоб
 , (7)
, (7)
де  - оптимальний фільтр для сигналів x(p) і g(p).
- оптимальний фільтр для сигналів x(p) і g(p).
Тоді, згідно (3) одержимо ідеальний регулятор для об'єктів із запізнюванням
 , (8)
, (8)
який називається
регулятором Ресвіка.
Внутрішній зворотний зв'язок регулятора Ресвіка, що містить ланку чистого запізнювання, прогнозує, який сигнал повинен з'явитися на виході об'єкта після чергової зміни керуючого впливу u. Тому що цей зв'язок позитивний, то прогнозований сигнал постійно компенсує (нейтралізує) рівний йому реальний вихідний сигнал об'єкта. Результуючий сигнал εр(p) з'являється тільки в перші моменти часу після зміни зовнішніх впливів. Таким чином, завдяки додатковому зворотному зв'язку, що моделює динаміку об'єкта, з основного контуру як би виключається чисте запізнювання  , що завжди погіршує стійкість системи й утрудняє рішення завдання синтезу.
, що завжди погіршує стійкість системи й утрудняє рішення завдання синтезу.
Як і в загальному випадку, практична реалізація ідеальної системи керування об'єктом із запізнюванням пов'язана з певними технічними труднощами. Істотним недоліком системи з регулятором (8) є її критичність або сильна чутливість до малих варіацій запізнювання об'єкта: система стійка тільки при точній рівності запізнювання об'єкта  й запізнювання
й запізнювання  , в об'єкті, який моделюється тобто
, в об'єкті, який моделюється тобто
 . (9)
. (9)
При розбіжності запізнювань система може стати нестійкою. Можна показати, що у випадку, коли Фопт(р) = kопт, для стійкості замкнутої системи необхідно kопт < 0,5. При kопт > 0,5 найменше порушення рівності (9) веде до втрати стійкості, хоча при точному збігу запізнювань коефіцієнт kопт може бути як завгодно більшим.
Для підвищення запасу стійкості систем з регулятором (8) у їхній контур уводять додаткові коригувальні ланки або обмежуються неповною компенсацією інерційної частини об'єкта. Природно, що динамічна точність керування при цьому погіршується.
Ідея нейтралізації запізнювання об'єкта реалізується також за допомогою
випереджувачу Сміта, яким охоплюють типові регулятори. Неважко переконатися, що при великому передатному коефіцієнті (
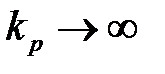
) регулятор з випереджувачем Сміта еквівалентний регулятору Ресвіка з
Фопт(р) =1.
Систему з випереджувачем Сміта технічно реалізувати легше, тому що не потрібно моделювати зворотну передатну функцію об'єкта.
Хоча регулятор Ресвіка (8) практично здійснити ніколи не вдається, аналіз його властивостей дозволяє оцінити граничні можливості керування об'єктами із запізнюванням. Так, для найкращого відтворення впливу, що задає, x(p) при відсутності перешкоди (тобто при Фопт(р) =1) регулятор (8) приймає вид:
 , (10)
, (10)
а передатні функції замкнутої системи за каналом завдання (x(p) - y(p))
 , (11)
, (11)
і за каналом збурювання (f(p) - y(p))
 . (12)
. (12)
Функціям (11) і (12) відповідають ідеальні перехідні процеси прямокутної форми, що закінчуються за мінімально можливий час  .
.
Найбільше важко керованими є об'єкти, що містять тільки чисте запізнювання
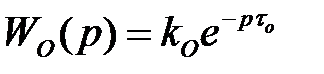 , (13)
, (13)
і для них найкраще застосовувати саме регулятор Ресвіка або випереджувач Сміта, що забезпечують структурну компенсацію запізнювання. Регулятор, (10) для об'єкта (13) приймає вид
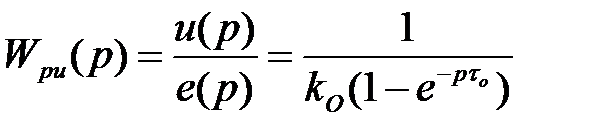 . (14)
. (14)
При повільних зовнішніх впливах, для яких припустима наближена заміна
 , (15)
, (15)
ідеальний регулятор еквівалентний І-Регулятору
 , (14)
, (14)
де kи = 1/ kо  .
.
Звідси можна сформулювати загальне правило настроювання регуляторів для об'єктів із запізнюванням:
передатний коефіцієнт регулятора повинен бути обернено пропорційний передатному коефіцієнту об'єкта й часу запізнювання.
 об'єкта керування, збурювання
об'єкта керування, збурювання  й
й  діючі на вході й виході об'єкта, а також перешкода g виникаюча в каналах завдання й виміру.
діючі на вході й виході об'єкта, а також перешкода g виникаюча в каналах завдання й виміру.


 , (1)
, (1)
 , тому корисна складова yu(p) на виході об'єкта буде повністю врівноважувати збурювання f(p).
, тому корисна складова yu(p) на виході об'єкта буде повністю врівноважувати збурювання f(p). .
.
 сигнал, що обчислюється на виході моделі
сигнал, що обчислюється на виході моделі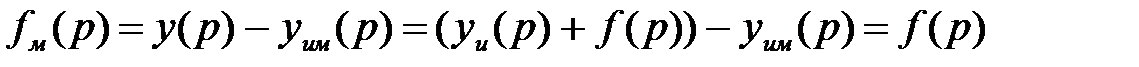
 . (2)
. (2) , що відповідає нульовим помилкам по каналах завдання й збурювання.
, що відповідає нульовим помилкам по каналах завдання й збурювання.
 , і крім того, - оптимальний фільтр Фопт(р). Замкнута система з таким регулятором теоретично еквівалентна ідеальній розімкнутій системі керування по збурюванню f(p), що практично миттєво відтворює завдання x(p) і повністю компенсує збурювання f(p). Передатна функція регулятора ідеальної системи
, і крім того, - оптимальний фільтр Фопт(р). Замкнута система з таким регулятором теоретично еквівалентна ідеальній розімкнутій системі керування по збурюванню f(p), що практично миттєво відтворює завдання x(p) і повністю компенсує збурювання f(p). Передатна функція регулятора ідеальної системи . (3)
. (3) прогнозує вплив керуючого впливу u(p) на керовану змінну y(p) (обчислює тридцятилітній yu(p) на виході об'єкта). Тому що сигнал yuм(p) з виходу прогнозуючої ланки надходить на вхід регулятора з позитивним знаком, те вся система після чергової зміни керуючого впливу виявляється як би розімкнутою. Внаслідок цього реальна замкнута система теоретично еквівалентна розімкнутій системі керування по збурюванню f(p).
прогнозує вплив керуючого впливу u(p) на керовану змінну y(p) (обчислює тридцятилітній yu(p) на виході об'єкта). Тому що сигнал yuм(p) з виходу прогнозуючої ланки надходить на вхід регулятора з позитивним знаком, те вся система після чергової зміни керуючого впливу виявляється як би розімкнутою. Внаслідок цього реальна замкнута система теоретично еквівалентна розімкнутій системі керування по збурюванню f(p). , (4)
, (4) , (5)
, (5) ;
; 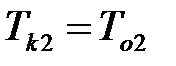 ,
, .
.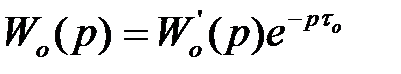 , (6)
, (6) - дрібно-раціональна функція, що характеризує інерційну частину об'єкта,
- дрібно-раціональна функція, що характеризує інерційну частину об'єкта,  - чисте запізнювання об'єкта.
- чисте запізнювання об'єкта. який відповідає ідеальному випереджувачу й точна реалізація якого технічно неможлива. Тому з метою спрощення шуканої структури регулятора й полегшення його технічної реалізації доцільно допустити, щоб для об'єктів, що містять чисте запізнювання
який відповідає ідеальному випереджувачу й точна реалізація якого технічно неможлива. Тому з метою спрощення шуканої структури регулятора й полегшення його технічної реалізації доцільно допустити, щоб для об'єктів, що містять чисте запізнювання  , ідеальна система відтворювала вплив, що задає, із
, ідеальна система відтворювала вплив, що задає, із  запізнюванням тобто Щоб
запізнюванням тобто Щоб , (7)
, (7) - оптимальний фільтр для сигналів x(p) і g(p).
- оптимальний фільтр для сигналів x(p) і g(p). , (8)
, (8)


 , що завжди погіршує стійкість системи й утрудняє рішення завдання синтезу.
, що завжди погіршує стійкість системи й утрудняє рішення завдання синтезу. й запізнювання
й запізнювання  , в об'єкті, який моделюється тобто
, в об'єкті, який моделюється тобто . (9)
. (9)

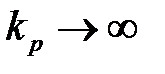 ) регулятор з випереджувачем Сміта еквівалентний регулятору Ресвіка з Фопт(р) =1.
) регулятор з випереджувачем Сміта еквівалентний регулятору Ресвіка з Фопт(р) =1.
 , (10)
, (10) , (11)
, (11) . (12)
. (12) .
.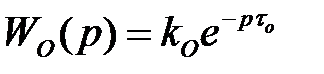 , (13)
, (13)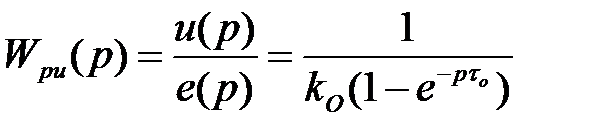 . (14)
. (14) , (15)
, (15) , (14)
, (14) .
.





