Приведем правило по которому можно найти производную сложной функции y = f(f(t)).
Теорема 3 (дифференцирование сложной функции). Пусть
функция x = f (t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = f (t). Тогда сложная функция y = f( f (t)) дифференцируема в точке t, причем справедлива формула
| (f (f(t))) ' = f' (x)f ' (t). | (3) |
Доказательство. Зададим x = f(t) отличное от нуля приращение D t. Этому приращению отвечает приращение D x = f (t+D t)-f (t) функции x = f(t). ПриращениюD x отвечает приращение D y = f(x+ D x)-f(x). Так как функция y = f(x)дифференцируема, то ее приращение D y представимо в виде (1):
D y =f' (x)D x + a (D x) D x,
где limD x® 0a (D x) = 0. Поделив данное выражение на D t ¹ 0, будем иметь:
D y/ D t=f' (x)D x/ D t+ a (D x)D x/ D t.
Из дифференцируемости функции x = f (t) в точке t вытекает, что
limD t ® 0D x/ D t = f ' (t).
Отметим, что из дифференцируемости функции x = f(t) следует, что D x® 0 при Dt® 0. Следовательно, limD t® 0a (D x) =0. Таким образом, получим необходимую формулу (3).
Пример 5. Найти y', если y = 5cos x.
y' = 5cos x (-sin x)ln 5=-5cos x sin x ln 5.
Для нахождения производной обратной функции существует следующее правило, а именно справедлива теорема
Теорема 4 (производная обратной функции). Пусть функция
y = f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x. Пусть, кроме того, эта функция дифференцируема в точке x и f'(x) ¹0. Тогда в некоторой окрестности соответствующей точки y = f(x) определена обратная функция x = f- 1 (y), причем обратная функция дифференцируема в точке x = f- 1 (y) и для ее производной справедлива формула
(f- 1(y)) ' = 1 /f' (x).
Доказательство. Так как функция y = f(x) строго монотонна и непрерывна в некоторой окрестности точки x, то существует обратная функция x = f-1(y), которая является строго монотонной и непрерывной в некоторой окрестности точки y = f(x).
Пусть D y¹ 0 приращение для y, а D x - соответствующее приращение обратной функции x = f-1(y). Тогда справедливо равенство
D x/ D y = 1 / (D y/ D x).
Переходя к пределу в последнем равенстве при D y® 0 и учитывая, что в силу непрерывности обратной функции D x® 0, получим
limD y ® 0D x/ D y = 1 / (limD x ® 0D y/ D x).
То есть, x'(y) = 1/y'(x).
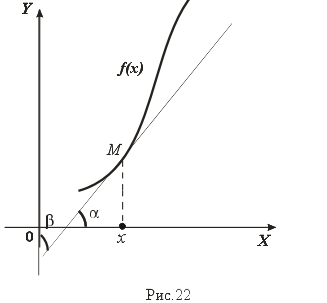
Доказанная теорема имеет простой геометрический смысл. Пусть M – точка графика функции f(x), (рис.22), производная f'(x) равна тангенсу угла наклона aкасательной, проходящей через M, к оси OX, а производная обратной функции (f-1(y))' в соответствующей точке y = f(x) равна тангенсу угла наклона b той же самой касательной к оси OY. Так как углы наклона a+ b=p/2, то формула нахождения производной обратной функции выражает очевидный факт: tgb = 1/tg a.
Пример 6. Найти x'y, если y = 2x3+3x5+x Имеем y' = 6x2+15x4+1, тогда x'y = 1/y'x = 1/(6x2+15x4+1).
Таблица производных простейших элементарных функций
Легко получить следующую таблицу производных основных элементарных функций, используя определение производной. Для более подробного изучения данного материала рекомендуем использовать, например, "Математический анализ" ч.1 В.А. Ильина, В.А. Садовничего, Бл.Х. Сендова.
- (u a(x))' = a u a-1(x) u '(x), в частности,
(1 /u (x)) ' = -u' (x) /u 2(x), (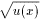
) ' = u' (x) / 2 ;
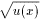2. (loga u (x))' = (u'(x)logae)/u(x) при 0<a¹1, u(x)>0, в частности, (ln u (x))' = u'(x)/ u (x);
3. (a u (x))' = a u (x)ln a u '(x) при 0<a¹1, в частности, (e u (x))' = u'(x)e u (x);
4. (sin u (x))' = cos u (x) u '(x);
5. (cos u (x))' = -sin u (x) u '(x);
6. (tg u (x))' = u '(x)/cos2 u (x) x¹ p/2+p n, n=0,+-1,...;
7. (ctg u (x))' = - u '(x)/sin2 u (x) x¹ p n, n=0,+-1,...;
8. (arcsin u (x))' = u '(x)/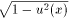 
, -1< u (x)<1;
9. (arccos u (x))' = - u '(x)/ 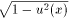, -1< u (x)<1;
10. (arctg u (x))' = u '(x)/(1+ u 2(x));
11. (arcctg u (x))' = - u '(x)/(1+ u 2(x)).
Введем гиперболические функции:
sh x = (1 / 2)(ex-e-x)- гиперболический синус;
ch x = (1 / 2)(ex+ex)- гиперболический косинус;
th x = sh x/ ch x -гиперболический тангенс;
cth x = ch x/ sh x - гиперболический котангенс.
Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных.
- (sh x) ' = ch x;
- (ch x) ' = sh x;
- (th x) ' = 1 / ch2 x;
- (cth x) ' = -1 / sh2 x.
Пример 7. Найти y', если
1. y(x) = x3arcsin x.
2. y(x) = ln sin (x2+1).
y' = (2 x cos(x 2+1)) / sin(x 2+1) = 2 x ctg (x 2+1)
Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций.
