Касательная к кривой y = f(x) в точке P(x1, y1) определяется уравнением
y = y1 + f'(x1)(x - x1),
где f'(x1) есть значение производной df/dx в точке x = x1 (рис. 6.1).

Если рассматриваемая кривая имеет в точке P вертикальную или почти вертикальную касательную, определение касательной при помощи этой формулы невозможно или затруднительно. Затруднения подобного рода легко преодолеваются, если для описания кривой используется неявное уравнение g(x, y) = 0. Тогда неявное уравнение касательной будет иметь вид:
gx(x1, y1)(x - x1) + gy(x1, y1)(y - y1) = 0,
где gx(x1, y1) и gy(x1, y1) суть значения производных д g/ д x и д g/ д y в точке P.
Пример. Касательная к окружности x2 + y2 - 1 = 0 в точке (1, 0) вычисляется следующим образом.
Поскольку g(x, y) = x2 + y2 - 1 = 0, то gx = 2x и gy = 2y, откуда следует, что gx(1, 0) = 2 и gy(1, 0) = 0. Таким образом, уравнение искомой касательной имеет вид 2(x - 1) + 0(y - 0) = 0, то есть касательная является вертикальной линией x = 1. Заметим, что если окружность или касательная записаны в явном виде, получить этот результат невозможно.
Явное выражение для нормали, восстановленной в точке P, имеет вид:
y = y1 - (x - x1)/f '(x1).
Это уравнение непригодно для случая, когда кривая горизонтальна в точке P. Соответствующее уравнение неявного вида записывается следующим образом:
gy(x1, y1)(x - x1) - gx(x1, y1)(y - y1) = 0.
Это уравнение позволяет определять нормали в тех случаях, когда применение явного уравнения невозможно или сопряжено с некоторыми трудностями.
| §2. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ | |||||
Напомним, что производной функции у = f (х) называется предел отношения приращения функции ∆у к приращению аргумента ∆х при стремлении ∆х к 0:
 Выведем ряд формул, облегчающих дифференцирование функций.
Выведем ряд формул, облегчающих дифференцирование функций.
| |||||
| 1.Производная постоянной величины. | |||||
Пусть f(x) = C = const. Тогда:
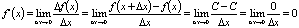 Т1: Производная постоянной величины равна 0:
Т1: Производная постоянной величины равна 0:
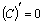
| |||||
| 2. Производная суммы двух функций. | |||||
| Т2: Пусть u = u(x) и v = v(x) – функции аргумента х. Пусть существуют u΄(x) и v΄(x). Тогда в точке х | |||||
| производная суммы функций равна сумме их производных | 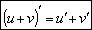
| ||||
| Введём вспомогательную функцию w(x) = u(x) + v(x). Её приращение в точке х: ∆w(x) = w(x+∆x) – w(x) = [u(x+∆x) + v(x+∆x)] – [u(x) + v(x)] = =[u(x+∆x) – u(x)] + [v(x+∆x) – v(x)] = ∆u(x) + ∆v(x). | |||||
Т.е. в точке х верно утверждение: ∆w = ∆u + ∆v.
Разделим обе части равенства на ∆х ≠ 0:
 .
При равенстве выражений, зависящих от Δх, равными должны быть и их пределы при стремлении ∆х к нулю: .
При равенстве выражений, зависящих от Δх, равными должны быть и их пределы при стремлении ∆х к нулю: 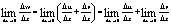
| |||||
Введём вспомогательную функцию
w(x) = u(x) · v(x).
Её приращение в точке х:
∆w(x) = w(x+∆x) – w(x) = [u(x+∆x) · v(x+∆x)] – [u(x) · v(x)] =
=[u(x) + ∆u(x)]∙[v(x) + ∆v(x)] – [u(x) ∙ v(x).
Воспользовались определением приращения функции:
∆u(x) = u(x+∆x) – u(x) => u(x+∆x) = u(x) + ∆u(x).
Тогда в точке х:
∆w = (u+∆u)(v+∆v) – uv = uv +u∆v + v∆u+∆u∆v – uv =>
∆w = u∆v + v∆u +∆u∆v.
Разделим обе части на ∆х и вычислим пределы от обеих частей равенства при ∆х → 0:
 Лемма: если функция дифференцируема в точке, то она в этой точке и непрерывна, т.е.
Лемма: если функция дифференцируема в точке, то она в этой точке и непрерывна, т.е.
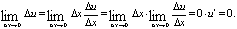 Используя теоремы о пределах, имеем окончательно:
Используя теоремы о пределах, имеем окончательно:
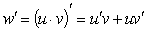 , ч. и т.д. , ч. и т.д.
| |||||
| Воспользовались теоремой: предел суммы равен сумме пределов, если таковые существуют. В соответствии с определением производной: w΄ = u΄ + v΄, ч. и т.д. | |||||
Эту теорему легко обобщить на случай большего числа функций одного аргумента:
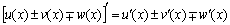
| 3. Производная произведения двух функций. | ||||
| Т3: Пусть u = u(x) и v = v(x) – дифференцируемые функции одного аргумента. Тогда в точке х | ||||
| производная произведенияфункций равна: | 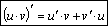
| |||
Введём вспомогательную функцию w(x) = u(x) · v(x).
Её приращение в точке х:
∆w(x) = w(x+∆x) – w(x) = [u(x+∆x) · v(x+∆x)] – [u(x) · v(x)] =
=[u(x) + ∆u(x)]∙[v(x) + ∆v(x)] – [u(x) ∙ v(x).
Воспользовались определением приращения функции:
∆u(x) = u(x+∆x) – u(x) => u(x+∆x) = u(x) + ∆u(x).
Тогда в точке х:
∆w = (u+∆u)(v+∆v) – uv = uv +u∆v + v∆u+∆u∆v – uv =>
∆w = u∆v + v∆u +∆u∆v.
Разделим обе части на ∆х и вычислим пределы от обеих частей равенства при ∆х → 0:
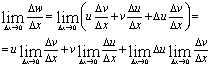 Лемма: если функция дифференцируема в точке, то она в этой точке и непрерывна, т.е.
Лемма: если функция дифференцируема в точке, то она в этой точке и непрерывна, т.е.
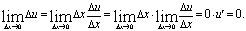 Используя теоремы о пределах, имеем окончательно:
Используя теоремы о пределах, имеем окончательно: 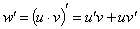 , ч. и т.д. , ч. и т.д.
| ||||
Следствие 1: постоянный множитель можно выносить за знак производной:
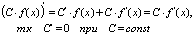 Следствие 2:
Следствие 2: 
| ||||
| 4. Производная частного двух функций. | ||||
| Т4: Пусть u = u(x) и v =v(x ≠0 – функции аргумента х. | ||||
| Пусть существуют u΄(x) и v΄(x). Тогда в точке х | ||||
| производная частного функций равна: | 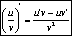
| |||
Введём вспомогательную функцию 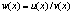 . .
| ||||
Её приращение в точке х:
 Воспользовались определением приращения функции:
∆u(x) = u(x+∆x) – u(x) => u(x+∆x) = u(x) + ∆u(x).
Тогда в точке х:
Воспользовались определением приращения функции:
∆u(x) = u(x+∆x) – u(x) => u(x+∆x) = u(x) + ∆u(x).
Тогда в точке х:
 Разделим обе части на ∆х и вычислим пределы от обеих частей равенства при ∆х → 0:
Разделим обе части на ∆х и вычислим пределы от обеих частей равенства при ∆х → 0:
 Напомним, что если функция дифференцируема в точке, то она в этой точке и непрерывна, т.е.
Напомним, что если функция дифференцируема в точке, то она в этой точке и непрерывна, т.е.

| ||||
| Используя теоремы о пределах, имеем окончательно: | 
| |||
5. Производная сложной функции.
Т5: производная сложной функции равна произведению производных функций, из которых она состоит (по соответствующим аргументам).
Пусть у = f(u), a u = g(x) и множество значений второй функции составляет область определения первой. Пусть существуют f΄(u) и g΄(x). Тогда:
 (Напомним, что для непрерывной функции u(x) при
Δx → 0 и Δu → 0).
П:
(Напомним, что для непрерывной функции u(x) при
Δx → 0 и Δu → 0).
П: 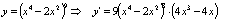 6. Таблица производных
6. Таблица производных
| ||||||||||
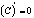
| 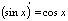
| 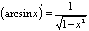
| ||||||||

| 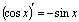
| 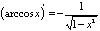
| ||||||||
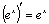
| 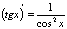
| 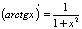
| ||||||||
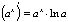
| 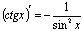
| 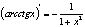
| ||||||||
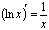
| 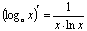
| |||||||||
| Правила дифференцирования: | ||||||||||
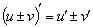
| 
| 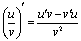
| ||||||||
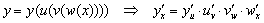
| ||||||||||
ПРОИЗВОДНАЯ
При некотором значении x функция имеет значение y = f (x). Этим значениям x и y на кривой соответствует точка M 0(x, y). Если аргументу x датьприращение D x, то новому значению аргумента x + D x соответствует новое значение функции y+ D y = f (x + D x). Соответствующей ему точкой кривой будет точка M 1(x + D x, y + D y). Если провести секущую M 0 M 1 и обозначить через jугол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что  .
.
Если теперь D x стремится к нулю, то точка M 1 перемещается вдоль кривой, приближаясь к точке M 0, и уголjизменяется с изменением D x. При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M 0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:
 .
.
Следовательно, f ´(x) = tga
т.е. значение производной f ´(x) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f (x) в соответствующей точке M 0(x, y) с положительным направлением оси Ox.






