Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение D x¹ 0, причем x+D x Î (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+D x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+D x,f(x+D x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (D x).
Определение 3. Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x ® 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.
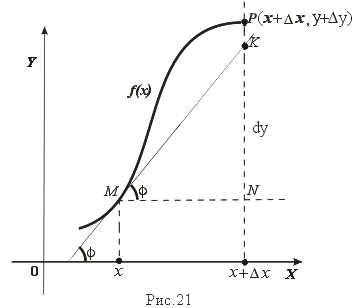
Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел limD x® 0f (D x) = f 0, который равен углу, образованному касательной с положительным направлением оси OX.
Справедливо утверждение:
Предложение 1. Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке
M(x,f(x)), причем угловой коэффициент этой касательной равен производной f'(x).
Из этого утверждения вытекает геометрический смысл производной: производная f'(x 0 ) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x 0, который в свою очередь равен tg угла наклона касательной к графику функции.
Тогда уравнение касательной к кривой f(x) в точке x0 имеет вид
y = f (x 0) +f' (x 0)(x-x 0)
Пример 3. Составить уравнение касательной к кривой y = 2x2-x+5 при x = -0,5.
Решение. Найдем производную в точке x = -0,5
y' = 4 x- 1, y' (-0,5) = -3.
Уравнение касательной имеет вид:
y = 6-3(x+ 0,5) или y = -3 x+ 4,5.
h4>Дифференцируемость функции Пусть функция определена на интервале (a,b).
Определение 4 (дифференцируемость в точке). Функция f(x) называется дифференцируемой в точке x, если приращение D y этой функции в точке x представимо в виде
| D y =A D x + a (D x) D x, | (1) |
где A - некоторое число, не зависящее от D x, а limD x® 0 a (D x) = 0.
В дальнейшем будем считать, что a(0) = 0. В этом случае функция a(x) будет непрерывной в точке D x = 0. Равенство 1 можно переписать иначе, так как функции a (D x), D x - бесконечно малые в точке D x = 0 и их произведение тоже бесконечно малая функция, поэтому
| D y =A D x +o (D x). | (2) |
Справедлива теорема
Теорема 1. Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на D x¹ 0 получим
D y/ D x = A+ a(D x).
Переходя к пределу в последнем выражении при D x® 0, получим, что A=f'(x).
Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел
limD x ® 0D y/ D x = f' (x).
Обозначим a(D x) = D y/ D x-f'(x). Отсюда вытекает представление (1).
Пример 4. Доказать, что функция |x| не дифференцируема в точке x = 0.
Решение. Найдем приращение функции в точке x = 0:
D y = | D x|
Поэтому
limD x ® -0D y/ D x = -1, limD x ® +0D y/ D x = 1,
следовательно, функция |x| в точке x = 0 не дифференцируема.
Следующая теорема выражает связь между непрерывностью и дифференцируемостью.
Теорема 2 (дифференцируемость и непрерывность). Если
функция дифференцируема в точке x, то она непрерывна в этой точке.
Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде (1), из которого следует, что limD x® 0D y = 0, что означает непрерывность функции в данной точке.
Заметим, что из непрерывности в данной точке не следует дифференцируемость в этой точке. Это видно из рассмотренного выше примера 4.
Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором множестве X, то функция называется гладкой на этом множестве. Если производная допускает конечное число точек разрыва (причем первого рода), то такая функция называется кусочно гладкой.
Правила дифференцирования
Приведем основные правила для нахождения производной:
- Производная постоянной равна нулю, то есть c' = 0.
- Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть
u (x)± v (x)) ' = u' (x)± v' (x).
3. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть
(u (x) v (x)) ' = u' (x) v (x) +u (x) v' (x).
Следствие 1. Постоянный множитель можно выносить за знак производной:
(cu (x)) ' = cu' (x).
4. Производная частного двух дифференцируемых функций может быть найдена по формуле
(u (x) /v (x)) ' = (u' (x) v (x) -u (x) v' (x)) /v 2(x)
при условии, что v(x)¹ 0.




