| «Математик, так же как художник или поэт, создает узоры». Г.Харди |
При выполнении вычислительных работ Вы почувствуете сами создание узоров или кружев геодезических вычислений в специальных расчётных ведомостях собственными руками и головой. Познаете красоту и неубиваемую логику в уравнивании результатов Ваших измерений и вычислений. На практике почувствуете, что такое невязка. Вы скажете, что Вы не математик. Это не так. В какое-то время Вам придётся им стать, чтобы получить на бумаге окончательные результаты в виде координат точек местности. И как в кружевах, если где-то неправильно был связан узелок, то придётся распускать последующее плетение, так и в расчётной ведомости, если неправильно будет определено какое-то значение, то придётся повторить необходимые расчёты. А узелками в ведомостях являются контрольные результаты в виде значений невязок, в виде контрольных сравнений полученных результатов с исходными их величинами. Вот эти узелки надо стараться не пропустить, чтобы заново не повторять Ваше геодезическое кружево. Это как раз одна из красот геодезии, строгое и обязательное контролирование своих действий.
Конечной целью построения съёмочного обоснования (теодолитного или полигонометрического хода) является получение координат его вершин: плановых х, у и высот Н.
В этом параграфе будет рассмотрен пример обработки разомкнутого теодолитного хода (рис. 7.22) с необходимыми пояснениями и указаниями. Обработка любого теодолитного хода производится несколькими этапами, каждый из которых выполняется с контролем искомых данных либо каких-либо промежуточных результатов. (Автор ещё раз напоминает Вам о необходимости контроля вычислений). В связи с этим целесообразно поэтапно теоретическую часть этого раздела совместить с практическим примером.
Все результаты обработки теодолитных ходов заносятся в ведомости установленной формы (ведомость вычисления координат – табл. 7.7; ведомость вычисления высот – табл. 7.8).
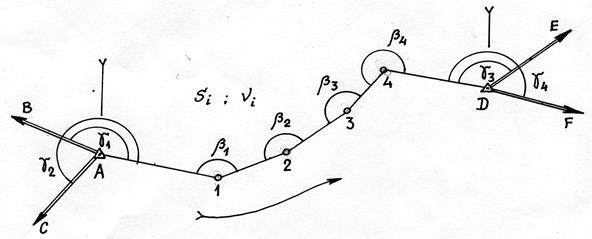
Рис.7.22. Разомкнутый теодолитный ход.
Таблица 7.3
Значения координат исходных пунктов
| Точки | А | В | С | D | E | F |
| Х, м | 5635,219 | 6235,814 | 4045,271 | 5578,703 | 7069,965 | 4189,684 |
| Y, м | 6081,327 | 4667,100 | 4777,253 | 6701,622 | 9593,387 | 8811,521 |
| Н, м | 142,754 | - | - | 168,440 | - | - |
Таблица 7.4
Значения примычных γ и горизонтальных β углов
| Обозначение | Значение примычного угла | Обозначение | Значение горизонтального угла |
| γ 1 | 182о35,2' | β 1 | 150о31,0' |
| γ 2 | 256о15,3' | β 2 | 163о07,5' |
| γ 3 | 124о39,1' | β 3 | 167о29,0' |
| γ 4 | 185о16,7' | β 4 | 241о21,5' |
Таблица 7.5
Значения углов наклона и наклонных расстояний
| Параметр | А-1 | 1-2 | 2-3 | 3-4 | 4-D |
| S, м | 189,65 | 113,96 | 121,58 | 93,46 | 164,04 |
| +4о36,5' | +2о27,0' | -0о43,7' | -2о11,3' | +4о08,0' |
В теодолитном ходе измерены горизонтальные углы β и γ (примычные) в вершинах хода, углы наклона линий и наклонные расстояния S. Значения координат исходных пунктов приведены в табл. 7.3, результаты полевых измерений представлены в табл. 7.4 и 7.5.
На приведённом рисунке показана классическая схема привязки разомкнутого теодолитного хода, когда на его конечных точках выполнена т.н. азимутальная привязка на два исходных направления.
Далее каждый из этапов обработки теодолитного хода рассмотрим раздельно.
79.1. Предварительные вычисления
Предварительные вычисления заключаются в азимутальной привязке начальной и конечной линий теодолитного хода к исходным направлениям, образованным пунктами Государственной геодезической сети, т.е. в определении дирекционных углов 
и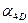 
. Для этого из решения обратной геодезической задачи, используя значения координат исходных пунктов (табл. 7.3), находят дирекционные углы (прямые и обратные) исходных направлений и дважды (контрольное второе вычисление) определяют значения искомых дирекционных углов через примычные углы (табл. 7.6).
Таблица 7.6
Предварительные вычисления дирекционных углов
| 
| 
| 
| |
| 
| 
| 
| |
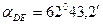
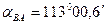
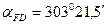
| dA1 = 189,04 | d12 = 113,86 | d23 = 121,57 | d34 = 93,39 | d4D = 163,61 |
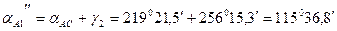
Допускается разность в полученных дирекционных углах до 1,0' (в примере разность допустима). Если это условие выполняется, то вычисляют среднее значение дирекционного угла:
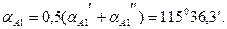
Аналогичные вычисления производятся и для дирекционного угла :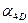
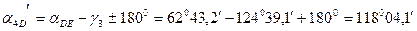
Разность дирекционных углов допустима.
Наклонные расстояния S приводят к горизонту (определяют горизонтальные проложения) по формуле (7.62)
.
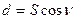Результаты вычислений для приводимого примера записаны в табл. 7.6.
79.2. Обработка результатов угловых измерений
Составим схему последовательной передачи дирекционных углов с начальной 
() на конечную 
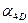() линии теодолитного хода, содержащего в общем случае n вершин (n горизонтальных углов β):
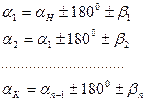(7.62)
В формулах (7.62) (+ β) – для левых по ходу углов, (– β) – для правых по ходу углов.
После сложения уравнений (7.62) получим:
- для левых по ходу углов:
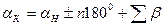; (7.63)
- для правых по ходу углов:
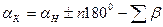. (7.64)
Поскольку и являются исходными (известными) дирекционными углами, то из формул (7.63) и (7.64) можно получить угловую погрешность (угловую невязку fβ), которая будет характеризовать качество выполнения угловых измерений:
- для левых по ходу углов:
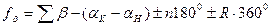; (7.65)
- для правых по ходу углов:
(7.66)
В формулы (7.65) и (7.66) введено слагаемое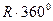 
(R = 1, 2, 3, …), необходимое для сокращения в невязках полных кругов, которые могут возникнуть в процессе суммирования углов.
Для технических теодолитных ходов установлена допустимая величина угловой невязки
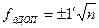, (7.67)
где n – число измеренных углов, использованных при вычислении невязки по формулам (7.65) или (7.66).
Выполнение условия
(7.68)
говорит о качественных угловых измерениях. В противном случае необходимо проверить полевые журналы либо повторить полевые измерения углов.
При выполнении условия (7.68) производят уравнивание углов введением в них поправок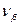 
поровну в каждый угол, считая измерения равноточными, со знаком, обратным знаку невязки:
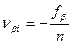. (7.69)
Здесь следует обеспечить равенство
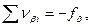(7.70)
которое может не получиться из-за округления поправок. Поправки необходимо округлять до 0,1', и, если равенство (7.70) не соблюдается, то в один из углов вводят дополнительную поправку: для углов, образованных короткими сторонами, поправку увеличивают, а для углов, образованных более длинными сторонами – поправку уменьшают.
После распределения поправок выполняют исправление (уравнивание) измеренных углов
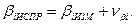(7.71)
Уравнивание углов контролируют выполнением следующих равенств:
- для левых по ходу углов:
(7.72)
- для правых по ходу углов:
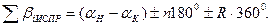(7.73)
Дирекционные углы сторон теодолитного хода вычисляют последовательно по формулам (7.62), используя в них исправленные значения горизонтальных углов (7.71). Контрольным вычислением является вычисленное значение , которое точно должно совпадать с его исходным значением, т.е.
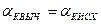. (7.74)
Пример 7.13. Обработка результатов угловых измерений.
Исходные данные по схеме рис. 7.22, табл. 7.3 – 7.5.
В ведомость координат (табл. 7.7) занести значения измеренных углов и горизонтальных проложений. Выписать значение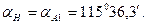 
Записать значения координат исходной точки А (ХА = 5635,219 = 5635,22 м; YA = 6081,327 = 6081,33 м).
По схеме рис. 7.22 видно, что измерены левые по ходу горизонтальные углы.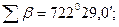 
( - ) = ( - ) = 
.
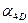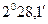. Невязка допустима (условие (7.68) выполнено). Контроль!
Таблица 7.7
