Часто такую работу приходится выполнять в тех случаях, когда не имеется возможности установить теодолит непосредственно на геодезическом знаке, т.е. выполнить центрирование непосредственно над вершиной измеряемого угла, которой является известная точка геодезического знака.
Рис. 7.15. Снесение координат с вершины геодезического знака на землю.
Для решения данной задачи от исходного пункта М (рис. 7.15) необходимо иметь в прямой видимости ещё один пункт (N) Государственной геодезической сети. Около пункта M выполняют разбивку двух базисов (основного и контрольного) b1 и b2, которые измеряют с относительной погрешностью 1:3000 – 1:5000 компарированной рулеткой или светодальномером. Базисы располагают таким образом, чтобы между направлениями 5M и 5N был угол порядка 90о, а треугольники АM5 и BM5 были примерно равносторонними. Во всяком случае измеряемые горизонтальные углы β1 – β4 необходимо выдержать в пределах 50о – 70о. Величины базисов должны быть порядка 60 – 100 м. При использовании для измерений рулетки было бы оптимальным, чтобы величина базиса не превышала длины рулетки.
На схеме снесения координат ломаная линия 4-5-6 является фрагментом теодолитного хода. При этом задачей снесения координат является не только определение координат точки 5, но и дирекционного угла, например, линии 5-6, т.е. решения полной задачи для элемента теодолитного хода.
Указанная задача решается после измерения базисов b1 и b2 и горизонтальных углов β1 – β6. При этом разбивка базиса b2 и все измерения, относящиеся к этому базису являются контрольным действием и обязательным для исполнения с целью обеспечения как необходимой точности определения координат точки 5 и дирекционного угла линии 5-6, так и для исключения возможной грубой погрешности, выявить которую при использовании только одного базиса не представляется возможным.
Углы βi измеряют теодолитом Т5 двумя полными приёмами либо теодолитами типа Т15 тремя полными приёмами с перестановкой лимба горизонтального круга между приёмами на 60о-90о. Целесообразно между полными приёмами выполнять повторное центрирование теодолита с целью приведения в измерениях погрешности центрирования к вероятностному характеру. В данном случае указанная погрешность будет входить в значение каждого из измеренных углов в вероятностной форме, т.е. не являться чисто систематической. После измерений и тщательной проверки полевых журналов вычисляют средние значения измеренных углов.
Последовательность дальнейшей обработки результатов измерений производится по приведенному ниже алгоритму.
1. Из решения обратной геодезической задачи находят значение дирекционного угла αMN и горизонтального проложения dMN исходного направления.
2. Вычисляют значения углов γ в точке М в соответствующих треугольниках АМ5 и ВМ5 как разность между измеренными углами и 180о.
3. По теореме синусов дважды находят значение стороны М5 и её среднее значение dМ5:
; 
; 
. (7.51)
4. По теореме синусов вычисляют значение угла β8
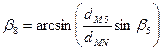(7.52)
и затем – значение угла
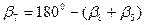. (7.53)
5. Из решения прямой геодезической задачи определяют координаты точки 5:
; 
, (7.54)
где 
для приведённой схемы.
6. Для контроля вычислений из решения обратной геодезической задачи определяют дирекционный угол направления N5 (
) и значение угла
. (7.55)
Полученное значение 
должно соответствовать его значению, вычисленному по формуле (7.53).
7. Передают дирекционный угол на определяемое направление 5-6:
. (7.56)
Далее приведем пример обработки результатов измерений при передаче координат с вершины геодезического знака на точку теодолитного хода по указанному выше алгоритму.
Пример 7.9. Снесение координат с вершины геодезического знака на землю.
Исходные данные (для схемы рис. 7.15):
ХА = 6235,756 м; YА = 4487,064 м; ХВ = 2183,641 м; YВ = 7216,442 м;
; 
; 
; 
; 
; 
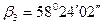. Значения базисов: b1 = 88,846 м; b2 = 80,552 м.
Решение.
1. Из решения обратной геодезической задачи: дирекционный угол направления MN
; горизонтальное проложение dMN = 4885,605 м.
2. Вычисляем значения углов γ в треугольниках (1) и (2):
γ(1) = 180о – (56o32'23" + 58o55'36'') = 64о 32' 01";
γ2 = 180o – (58o24'02'' + 60o45'06'') = 60о 50' 52".
3. По формулам (7.51) дважды (из двух треугольников) находим горизонтальное проложение линии M5:
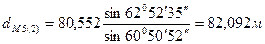
Разница в значениях dM5 составляет 0,006 м, что допустимо для расстояния 82 м, поскольку относительная погрешность в этом случае составит примерно 1:13700.
4. Вычисляем значения углов β7 и β8:
;
5. Вычисляем значения координат точки 5 теодолитного хода.
Дирекционный угол направления М5
6. Контрольное вычисление.
Из решения обратной геодезической задачи значение дирекционного угла направления N5 
Значение 
, что совпадает с вычисленным ранее значением.
7. Выполняем передачу дирекционного угла на определяемую линию 5-6 теодолитного хода:
Рис. 7.16. Привязка теодолитного хода к стенным геодезическим знакам.
