Эффузией называют процесс истечения разреженного газа из отверстия, характерные размеры которого много меньше длины свободного пробега молекул.
Пусть имеется заполненный разреженным газом сосуд, разделённый перегородкой с небольшим отверстием. Размер отверстия и толщина перегородки намного меньше длины свободного пробега молекул газа.
Если стенки одной части сосуда поддерживать при температуре Т 1, а другой – при температуре Т 2, то плотность потока молекул из первой части сосуда во вторую и наоборот можно определить по формулам
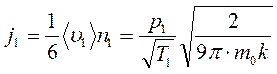и 
.
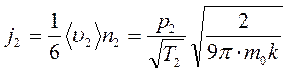Если газ в двух частях сосуда находится в равновесии то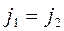 
и получаем:
.
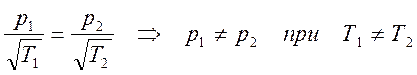Видно, что условие равновесия для разреженного газа существенно отличается от условия равновесия для неразреженного газа, длина свободного пробега молекул которого много меньше характерного размера отверстия в перегородке сосуда. Для неразреженного газа равновесие наступает при равенстве давлений в обеих частях сосуда.
Физический вакуум
Когда длина свободного пробега молекул превышает характерный размер сосуда, говорят, что достигнут вакуум, и газ находится в состоянии ультраразряжения.
Поведение ультраразреженного газа существенно отличается от поведения газов при обычных условиях. Отсутствует внутреннее трение (вязкость) и теплопроводность газа.
Вакуум – понятие относительное: условие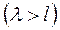 
может иметь место в малых порах даже при атмосферном давлении.
В технике обычно принимают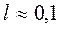 
м.
Мерой степени разрежения газа служит отношение средней длины свободного пробега молекул газа и характерного линейного размера сосуда, в котором находится газ:
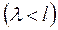– низкий вакуум
– средний вакуум
– высокий вакуум.
| Характеристика | Вакуум | |||
| Давление, мм. рт. ст. | низкий 760 – 1 | средний 1 – 10-3 | высокий 10-3 – 10-8 | сверхвысокий 10-8 и менее |
| Концентрация, м-3 | 1025 – 1022 | 1022 - 1015 | 1019 – 1014 | 1014 и менее |
Зависимость от давления коэффи-
циентов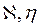 
| Не зависит от давления | Определя- ются пара- метром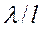 
| Прямо про- порциональ- ны давлению | Теплопровод- ность и вяз- кость практи- чески отсутс- твуют |
Броуновское движение
Броуновским движением называют хаотическое движение мельчайших частиц в жидкости или газе.
Для описания броуновского движения частицы в жидкости предполагают, что на неё со стороны частиц жидкости действует случайная сила ξ, среднее значение которой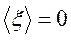 
. Уравнение движения броуновской частицы в направлении выбранной оси ОХ имеет вид:
, где
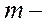масса броуновской частицы;
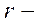коэффициент вязкого трения броуновской частицы в жидкости.
После усреднения этого уравнения и с учётом того, что
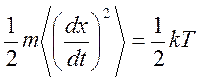
Эйнштейном была получена формула:
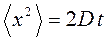, где
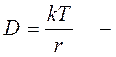коэффициент диффузии броуновской частицы.
Из формулы Эйнштейна следует, что квадрат перемещения броуновской частицы пропорционален времени, прошедшему с начала наблюдения за ней, а за одинаковые промежутки времени его значение увеличивается с повышением температуры Т и уменьшается с возрастанием коэффициента вязкого трения r.
Экспериментальное исследование броуновского движения позволило Перрену вычислить значение постоянной Больцмана k.
Статистический метод, используемый при создании теории броуновского движения, используется для решения целого ряда прикладных задач, например, для анализа точности работы различных систем управления.
Лекция 16
