При работе тепловой машины рабочее тело совершает замкнутый термодинамический цикл. При этом не вся произведённая работа становится полезной – часть её теряется, переходя в теплоту в холодильнике.
Максимальным КПД обладает тепловая машина, в которой цикл рабочего тела состоит только из равновесных тепловых процессов – изотерм и адиабат и, следовательно, является обратимым. Простейший равновесный круговой процесс, состоящий из двух изотерм и двух адиабат, получил название цикла Карно.
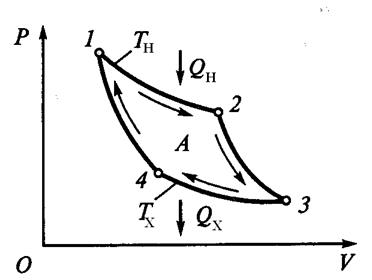При первом изотермическом процессе 1–2 происходит передача рабочему телу теплоты Q H, причём передаётся она бесконечно медленно при практически нулевой разности температур нагревателя и рабочего тела. Далее рабочее тело подвергается адиабатическому расширению без теплообмена с окружающей средой (процесс 2–3). При последующем изотермическом процессе 3–4 холодильник получает от рабочего тела теплоту Q X. Процесс 4–1 представляет собой адиабатическое сжатие, переводящее рабочее тело в первоначальное состояние.
Рассчитаем КПД цикла Карно для ν молей идеального газа. Для адиабат 2–3 и 4–1 получаем:
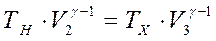и 
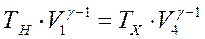
После деления одного равенства на другое имеем
.
Так как процессы 1 – 2 и 3 – 4 являются изотермическими, то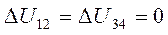 
. Следовательно
;
.
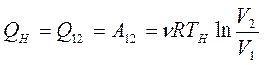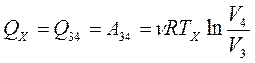Для КПД получаем
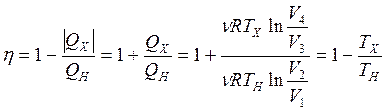или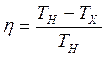 
.
Для холодильной машины и теплового насоса, работающих по циклу Карно на идеальном газе, имеем
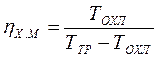и 
.
Тепловую машину, работающую по циклу Карно, называют идеальной тепловой машиной, так как в ней достигается максимально возможный КПД при заданном перепаде температур между нагревателем и холодильником.
На практике построить идеальную тепловую машину невозможно. Если процессы считать строго изотермическими, то при их протекании рабочее тело не должно нагреваться от нагревателя и охлаждаться холодильником.
Теоремы Карно:
1. КПД любой тепловой машины, работающей по обратимому циклу Карно, не зависит от природы рабочего тела и устройства машины, а является функцией только температур нагревателя и холодильника.
2.КПД любой тепловой машины, работающей по необратимому циклу, меньше КПД тепловой машины с обратимым циклом Карно при условии равенства температур их нагревателей и холодильников:
.
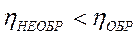Вторую теорему Карно можно обосновать тем, что при необратимом круговом процессе неизбежно произойдёт преобразование части работы в теплоту вследствие происходящих внутри машины диссипативных процессов.
Неравенство Клаузиуса
Совместное применение первой и второй теорем Карно позволяет получить следующее неравенство:
или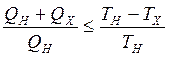 
.
Тогда
.
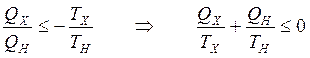Рассмотрим тепловую машину, рабочее тело которой при совершении кругового термодинамического процесса обменивается теплотой с достаточно большим числом тепловых резервуаров (нагревателей и холодильников), имеющих температуры Т 1, Т 2, Т 3, …, Ti, …, ТN. При этом рабочему телу от тепловых резервуаров передаётся количество теплоты Q 1, Q 2, Q 3, …, Qi, …, QN. Величины Qi могут иметь отрицательный знак в случае, если при теплообмене с i -м резервуаром теплота отводится от рабочего тела.
Для такой тепловой машине можно записать
или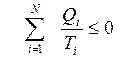 
.
Величину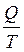 
называют приведённым количеством теплоты.
При переходе к бесконечному числу тепловых резервуаров, с которыми рабочее тело тепловой машины обменивается теплотой, суммирование можно заменить интегрированием по замкнутому термодинамическому циклу:
.
Это неравенство называют неравенством Клаузиуса.
Если термодинамический цикл состоит только из обратимых процессов, это неравенство переходит в равенство Клаузиуса:
.
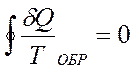