Оценки  (
( ) и
) и  (S) поданных за класс
(S) поданных за класс  (u = 1,2,…, l) по фиксированному опорному множеству или системе опорных множеств соответственно.
(u = 1,2,…, l) по фиксированному опорному множеству или системе опорных множеств соответственно.
Дадим интерпретацию рассмотренных этапов задания алгоритма (Г-модели) применительно к задаче классификации.
Пусть заданы объекты двух классов:
первого  ,
,  ,…,
,…, 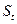 и
и
второго 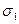 ,
, 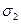 ,…,
,…,  .
.
Каждый из объектов характеризуется набором значений u бинарных признаков. Требуется отнести предъявленную строку S длины u к одному из классов.
Зададим длину опорного множества  , равную K и выделим все наборы столбцов длины K (предполагается, что всё множество объектов с u признаками сведено в таблицу T mn2).
, равную K и выделим все наборы столбцов длины K (предполагается, что всё множество объектов с u признаками сведено в таблицу T mn2).
Берем первый по порядку набор, составленный из столбцов с номерами 1,2,…,k. В предъявленной строке S и строках  ,
,  ,…,
,…, 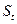 и
и 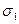 ,
, 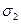 ,…,
,…,  выделим только первые k столбцов (это возможно, т.к. перестановка столбцов в исходной таблице не приводит к потери информативности заданных описаний).
выделим только первые k столбцов (это возможно, т.к. перестановка столбцов в исходной таблице не приводит к потери информативности заданных описаний).
Полученные после такой операции строки обозначим через  ,
,  ,…,
,…,  и
и  ,
, 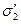 ,…,
,…,  ;
;  .
. 
Обозначим через  число строк из
число строк из  ,
,  ,…,
,…,  совпадающие с
совпадающие с  , через
, через  - число строк из
- число строк из  ,
, 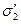 ,…,
,…,  , тоже совпавшие с
, тоже совпавшие с  .
.
Построим величины  и
и  для всех наборов
для всех наборов  ,
,  ,…,
,…,  длины k (эти величины соответствуют оценкам
длины k (эти величины соответствуют оценкам  (
( ) и
) и  (
( )).
)).
Тогда оценки
 (S) =
(S) = 

и
 (S) =
(S) = 

полученные по всем наборам длины k, естественно назвать числом голосов, поданных строкой S соответственно за первый и второй классы.
Отнесение строки S к одному из классов можно провести одним из рассмотренных ранее решающих правил. Кроме того, следует учитывать удельное число голосов. Например, величины  и
и  называют удельным числом голосов, поданных за первый и второй классы строкой S.
называют удельным числом голосов, поданных за первый и второй классы строкой S.
Если  >
>  , то строку S можно отнести к первому классу. При
, то строку S можно отнести к первому классу. При  =
=  = 0 – алгоритм отказывается от классификации строки S. Если же число объектов в обоих классах совпадает, то нет необходимости привлекать при отнесении (классификации) удельное число голосов.
= 0 – алгоритм отказывается от классификации строки S. Если же число объектов в обоих классах совпадает, то нет необходимости привлекать при отнесении (классификации) удельное число голосов.
В случае, если решающее правило ориентировано на использование параметров  и
и  ,
,
 =
=  (S) -
(S) -  (S);
(S);
 =
=  (S) /
(S) /  (S); то значение
(S); то значение  и
и  можно выбрать в процессе обучения (на контрольном материале) следующим образом:
можно выбрать в процессе обучения (на контрольном материале) следующим образом:
- фиксируются некоторые значения  и
и  .
.
- производится прогноз на контрольном материале.
- за каждый неправильный прогноз и отказ от распознавания начисляются штрафные очки (например, 2 и 1).
- подсчитывается общее число штрафных очков.
- осматривается окрестность  и
и  и каждый раз подсчитывается сумма штрафных очков.
и каждый раз подсчитывается сумма штрафных очков.
- осуществляется переход в точку с минимальным числом штрафных очков и т.д. до нахождения оптимальных  и
и  .
.
Пример:
Пусть задана таблица  объектов (m = 6; n
объектов (m = 6; n  6; l = 2).
6; l = 2).

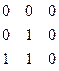
 объекты класса
объекты класса 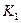



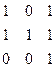 объекты класса
объекты класса 

 - строка S
- строка S
В качестве голосующих наборов рассмотрим наборы столбцов <1,2>, <3,4>, <5,6>. Две строки будем считать похожими, если они совпадают.
Оставим в таблице сначала столбцы 1и 2, затем 3 и 4 и, наконец, 5 и 6. Получаем, что число совпадений  со строками первого класса равно 1, второго 2, т.е.
со строками первого класса равно 1, второго 2, т.е.  = 1;
= 1;  = 2. Аналогично
= 2. Аналогично  = 2;
= 2; 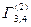 = 1;
= 1;  = 1;
= 1;  = 0.
= 0.
Следовательно,  (S) = 4;
(S) = 4;  (S) = 3.
(S) = 3.
Если решающее правило относит строку по простому большинству голосов, то в данном примере строка будет относиться к классу 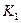 , т.к.
, т.к.  (S) >
(S) >  (S). При
(S). При  = 1 строка S также будет отнесена к классу
= 1 строка S также будет отнесена к классу 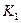 ; т.к. (
; т.к. ( (S) -
(S) -  (S)) = 1 =
(S)) = 1 =  удельное число голосов, поскольку
удельное число голосов, поскольку  =
=  .
.






