Своевременное и полное обеспечение техники запасными частями является необходимым условием для повышения эффективности ее использования. Так, по данным хронометражных наблюдений, 10-25% рабочего времени полевые агрегаты простаивают из-за технических неисправностей. В свою очередь, среднее время восстановления технического устройства (Тв) можно представить в виде Тв = Та + Тад + Тп, где Та – среднее время активного ремонта, включая поиск неисправного элемента; Тад – среднее время простоя из-за административных факторов; Тп - – среднее время простоя из-за отсутствия необходимых запасных элементов. Как показывает опыт, среднее время простоя оборудования из-за отсутствия запасных частей нередко составляет 40-50% всего времени простоя по техническим причинам.
Желание исключить простой техники приводит к чрезмерно большому комплекту запасных элементов. Так, анализ затрат на проведение работ в сельском хозяйстве показывает, что существенная доля их идет на амортизационные отчисления (капитальный ремонт и реновация). Значительная часть этих средств расходуется на приобретение запасных частей (до 40% и более). Поэтому создание большого запаса элементов экономически нерационально. Решение вопроса об оптимальном обеспечении машин и оборудования запасными частями связано с компромиссным удовлетворением указанных тенденций при достижении максимума народнохозяйственного эффекта.
2. Практическая методика определения оптимального количества запасных частей, хранящихся у потребителя
Пусть для определения периода эксплуатации t требуется обеспечить техническое устройство оптимальным количеством запасных элементов (компонент). Пополнение запаса происходит через промежуток времени r, причем среднее время доставки запасных частей с центральной базы tg<<r, поэтому можно считать, что r = t. Предполагается, что запасные компоненты находятся в режиме не нагруженного резерва и законы распределения спроса по каждой позиции номенклатуры и их характеристики известны.
Зная закон распределения спроса на запасные части, его характеристики легко определить необходимое количество запасных частей на складе при заданной вероятности удовлетворения спроса.
Во многих случаях можно с высокой точностью предсказать вероятность отказа рабочих элементов в зависимости от времени и режима работы аппаратуры[1] и оценить необходимое количество запасных элементов для заданной вероятности удовлетворения спроса.
Обычно при определении необходимого количества запасных частей задаются вероятностью Р удовлетворения спроса. Но, естественно возникает вопрос: почему Р принято, например, равным, 0,95, а не 0,8 или 0,9? Как найти экономически обоснованную величину вероятности удовлетворения спроса? Ведь в зависимости величины Р будут существенно изменяться и величина запаса и коэффициент готовности технического устройства. Чтобы ответить на поставленный вопрос, представим процесс функционирования технического устройства (ЭВМ, металлорежущего станка, комбайна, р/релейной станции и т.п.) как циклический (замкнутый) процесс смены состояний.
Граф состояний рассматриваемой технической системы представлен на рис.2.1


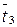
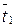

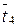
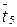
Рисунок 2.1 – Граф состояний технической системы
Здесь S1 – исправное состояние оборудования, работа; S2 - простой, поиск неисправности; S3 – ремонт при наличии детали на складе; S4 – ремонт при отсутствии необходимой детали на складе (деталь получена на центральной базе); S5 – простой из-за административных и др. факторов; 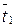 – среднее время поиска неисправностей;
– среднее время поиска неисправностей;  - среднее время поиска неисправностей;
- среднее время поиска неисправностей; 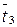 - среднее время ремонта при наличии деталей на складе;
- среднее время ремонта при наличии деталей на складе; 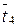 - среднее время ремонта при получении детали с центральной базы;
- среднее время ремонта при получении детали с центральной базы; 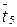 - среднее время простоя из-за административных и др. факторов; P – принятая вероятность удовлетворения спроса на запасные части.
- среднее время простоя из-за административных и др. факторов; P – принятая вероятность удовлетворения спроса на запасные части.
Решив систему уравнений для предельных вероятностей, найдем, что

 =
= 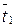 / [
/ [ 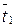 +
+  + p
+ p  + (1- p)
+ (1- p)  +
+ 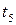 ], (1)
], (1)
где:  - средняя доля времени, которую оборудование приводит в состояние S1;
- средняя доля времени, которую оборудование приводит в состояние S1;
если  + p
+ p 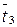 + (1- p)
+ (1- p) 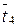 +
+ 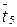 ; то
; то
 = К г – коэффициент готовности оборудования.
= К г – коэффициент готовности оборудования.
Воспользовавшись полученной зависимостью  = f(p), найдем оптимальную по критерию народнохозяйственной эффективности вероятность удовлетворения спроса и, соответственно, оптимальное количество запасных частей на складе.
= f(p), найдем оптимальную по критерию народнохозяйственной эффективности вероятность удовлетворения спроса и, соответственно, оптимальное количество запасных частей на складе.
Алгоритм расчета. Для фиксированных значений вероятности удовлетворения спроса  (например,
(например,  = 0,999;
= 0,999;  = 0,99 и т.д.) определяется:
= 0,99 и т.д.) определяется:
1. Необходимое количество запасных частей по каждой i -ой позиции номенклатуры  {
{  = f(
= f(  ), i=1,…,N } и их стоимость
), i=1,…,N } и их стоимость  =
=  ·
·  , где
, где  - “вес” (стоимость) одного запасного элемента i -го типа.
- “вес” (стоимость) одного запасного элемента i -го типа.
2. Общая стоимость запаса сменяемых компонент  =
= 
 .
.
3. Вероятность удовлетворения спроса по всем позициям номенклатуры  =
=  (в общем случае на все
(в общем случае на все 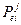 =
= 
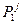 ).
).
4. Вероятность пребывания технического устройства в работоспособном состоянии 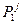 (по формуле (1)).
(по формуле (1)).
5. Объем продукции, произведенной на машине за время r = t (при условии, что отсутствуют простои по технологическим, из-за профилактического обслуживания и другим причинам).
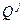 = Пф ∙
= Пф ∙ 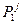 ∙t,
∙t,
где: Пф – фактическая производительность технического устройства на единицу чистого времени.
6. Убытки от мобилизации средств в запасы 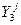 =
= 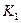 ∙
∙  . Если принять, что
. Если принять, что 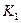 = Ен, то
= Ен, то 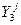 = Ен ∙
= Ен ∙  , где Ен - нормативный коэффициент эффективности капитальных вложений.
, где Ен - нормативный коэффициент эффективности капитальных вложений.
7. Расходы на хранение запаса 


 .
.
8. Убытки от увеличения прямых эксплуатационных затрат на производство единицы продукции 3е при снижении величины 
 = (
= ( -
-  )
) 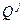 = Сп (
= Сп ( -
- 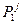 ) Пф∙ t,
) Пф∙ t,
где: С п - условно постоянные расходы, приходящиеся на одно изделие.
9. Затраты на приобретение запасных частей на центральной базе, включая транспортные расходы


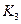 (1-
(1-  ).
).
10. Убытки от уменьшения объема выпуска продукции при снижении
 =
= 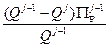

 (
(  -
- 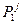 ),
),
где:  - прибыль от реализации
- прибыль от реализации 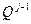 единиц продукции;
единиц продукции;
 ,…,
,…,  - коэффициенты, зависящие от местных условий.
- коэффициенты, зависящие от местных условий.
11. Оптимальный объем запасных элементов по критерию минимума суммарных потерь (см. табл. 1)
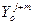 =
=  +
+  +
+ 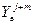 +
+ 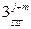 +
+  .
.
Если известна зависимость функции надежности R от количества и структуры запасных компонент R = f(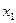 ,...,
,...,  ), то для фиксированных значений
), то для фиксированных значений  определяется минимальный по стоимости объем запаса[2]. Далее следуют процедуры, описанные в пп. 4-11.
определяется минимальный по стоимости объем запаса[2]. Далее следуют процедуры, описанные в пп. 4-11.
Таблица 1
Приня-тая веро- ятность удовле-тво-рения спроса
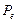
| Общая стои-мость запас-ных компо-нент, хранящихся у по-треби-теля W | Вероят-ность удов-летворе-ния спроса по всем позици-ям но-менкла-туры, Р (вероят-ность возник-новения дефици-та за время t 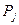 =1-p) =1-p)
| Веро-ятность пре-быва-ния техни-ческо-го уст-ройст-ва в ра-бото-спосо-бном состо-янии

| Объем про-дукции (или рабо-ты) произ-веден-ной на обору-дова-нии за время t Q | Убыт-ки от моби-лиза-ции сре-дств в запасы
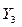
| Рас-ходы на хра-не-ние за-пас-ных час-тей

| Убытки от увели-чения прямых эксплу-атаци-онных затрат на про-изводст- во еди-ницы продук-ции
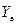
| Затраты на приобре-тение за-пасных компо-нент на централь-ной базе, включая тран-спортные расходы

| Убы-тки от уме-ньше-ния объе-ма вы-пуска про-дук-ции

| Суммарные убытки
 = =  + + 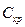 + + 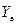 + +  + + 
|
| - | - | - | - | - | - | - | - | - | - | - |

| 
| 
| 
| 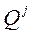
| 
| 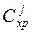
| 
| 
| 
| 
|
| - | - | - | - | - | - | - | - | - | - | - |
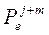
| 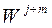
| 
| 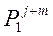
| 
| 
| 
| 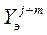
| 
| 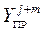
| 
|
При известном законе распределения спроса на запасные части и наличии информаации о прежнем спросе для определения оптимального количества запасных частей на складе можно использовать Байесовский подход. Так, допустим, что для данного месяца существует вероятность 0,65, что для удовлетворения спроса будет достаточно заказать одну партию запасных частей, и вероятность 0,35, что понадобится заказать 2 партии. Средний доход от каждой необходимой партии составляет 100 руб., а затраты на приобретение и хранение – 50 руб. Предположим также, что решение заказать еще одну партию может быть принято в начале второй декады. Кроме того, если понадобится только одна партия, то существует вероятность 0,2, что половина запасных частей к этому времени будет использована; если же понадобится 2 партии, то имеется вероятность 0,6,что к началу второй декады будет использовано более половины запасных частей.
 Посмотрим, какое следует принять решение относительно величины заказа, используя критерий математического ожидания прибыли, если стало известно что к началу второй декады использована половина всех запасных частей. Апостериорные вероятности того, что понадобится 1 партия (P(A/B))или две партии (P(A/B)) запасных частей можно вычислить по формуле Байеса.
Посмотрим, какое следует принять решение относительно величины заказа, используя критерий математического ожидания прибыли, если стало известно что к началу второй декады использована половина всех запасных частей. Апостериорные вероятности того, что понадобится 1 партия (P(A/B))или две партии (P(A/B)) запасных частей можно вычислить по формуле Байеса.
P(A/B) =  = 0,38
= 0,38
P(A/B) = 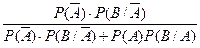 =0,62.
=0,62.
Полученные апостериорные вероятности используем для вычисления математического ожидания прибыли для обоих вариантов решения:
| Необходимое число партий | Заказана одна партия | Заказано две партии | ||||
| Прибыль X | Вероят-ность P(X) | X∙P(X) | Прибыль X | Вероят-ность P(X) | X∙P(X) | |
| 0,38 | 0,38 | |||||
| 0,62 | 0,62 |
 ∙ P(X) = 50 руб.
∙ P(X) = 50 руб.  ∙ P(X) = 62 руб.
∙ P(X) = 62 руб.
Таким образом, решение, максимизирующее математическое ожидание прибыли, представляет планирование заказать 2 партии запасных частей и т.д.
В условиях функционирования АСУП накопление и обработку информации о расходе запасных частей, а также все расчеты по выработке оптимальной стратегии управления объемом запасных частей целесообразно выполнять на ЭВМ.
Тема 11: Алгоритмы классификации (распознавания), основанные на вычислении оценок ППП
Общие определения.






