Цель любого выборочного исследования состоит в том, чтобы, сформировав выборку, собрать по ней информацию и на основе этой информации оценить искомые характеристики генеральной совокупности.
Наиболее распространенной в социологических исследованиях задачей является оценка среднего значения признака (или доли в случае качественного признака) в генеральной совокупности.
Проиллюстрируем на примере нахождение выборочной оценки среднего генеральной совокупности. Предположим, что оценивается среднее число газет и общественно-политических журналов, выписываемых сотрудниками некоторого производственного коллектива. Рассмотрим по порядку все необходимые операции и их результаты.
Составляется основа выборки, т. е. список всех единиц отбора. В качестве такой основы может быть взят алфавитный список всех сотрудников, пронумерованных последовательно (табл. 15). В целях наглядности вместе с основой выборки приводятся и все истинные значения единиц отбора, еще неизвестные исследователю. В дальнейшем сопоставим истинное значение искомого параметра и выборочную оценку.

Общая сумма выписываемых газет и журналов равна 150. Среднее число выписываемых газет и журналов на каждого сотрудника равно = 150/50 = 3.
Среднее квадратическое отклонение для генеральной совокупности равно

Сумма квадратов отклонений равна 146 при условии, что одно значение квадрата отклонения, а именно от единицы отбора 28, было исключено из суммы. Это значение, равное 49, резко увеличивает сумму, будучи нетипичным для генеральной совокупности.
Такое «исключение» экстремального отклонения нередко применяется при обработке первичной социальной информации в том случае, когда предусмотрено возведение в квадрат, а само отклонение в 2—3 раза превышает среднее значение параметра.
Однако ни среднее значение параметра, ни среднее квадратическое отклонение перед началом исследования не известны. В противном случае само исследование было бы излишним.
Естественно предположить при анализе вышеприведенного примера, что каждый респондент (единица отбора и единица наблюдения) выписывает несколько газет и журналов и что количество выписываемых газет и журналов не слишком сильно варьирует (если бы путем выборочного исследования потребовалось определить, скажем, объем личных библиотек, положение исследователя осложнилось бы). Исходя из этих соображений, полагаем достаточной выборку, состоящую из пяти респондентов. Проверить правильность определения объема выборки можно только после обработки результатов пилотажного исследования.
Предположим, что случайный выбор из табл., 15 дал следующие результаты: выбраны номера 18, 4, 28, 39, 22; они соответствуют Значениям признаков 4, 0, 10, 4, 4.
Среднее арифметическое но выборке х = 22/5 = 4,4, дисперсия

Такое значительное отклонение от истинного значения средней объясняется тем, что в выборку попал респондент № 28, исключенный при подсчете дисперсии для генеральной совокупности как нетипичный. Однако при формировании выборки еще неизвестно, что данный респондент нетипичен. Но сам факт, что среднее квадратическое отклонение приближается по величине к средней, должен насторожить исследователей.
Для большей наглядности выразим s в процентах от величины средней: (3,5:4,4) • 100%= 79%, т. е. среднее отклонение значений признака от выборочной средней арифметической величины «оставляет 79%. В таких случаях целесообразно увеличить объем выборки, например, в 2 раза. В результате были отобраны номера: 44, 2, 12, 26, 14, 27, 35, 9, 8, 49; значения признака 5, 2, 4, б, 1, -3,2,5,3, 4.
Среднее арифметическое — 3,6, дисперсия s2 = 2,26, среднее квадратическое отклонение s = 1,5. Теперь оно составляет приблизительно 40% от величины средней. При больших дисперсиях объем выборки увеличивают с учетом практических возможностей до тех пор, пока дисперсия не перестает уменьшаться. Дальнейшее увеличение объема выборки является нецелесообразным. Обычно исследователь приходит к некоторому компромиссному решению относительно объема выборки в зависимости от требуемой точности, атакже средств и времени, которыми он располагает.
Сводка необходимых формул для простой случайной выборки. В рассмотренном гипотетическом примере легко было оценить качество выборочной оценки среднего (перед глазами была информация дня обо всей генеральной совокупности). Но как провести его оценку в реальном исследовании, когда имеется только информация, полученная из выборки?
На помощь приходит статистическая теория выборочного метода. Она позволяет при условии реализации случайного отбора достичь, по крайней мере, следующих двух целей:
1. По заданной априори необходимой степени точности выводов (формализуемой с помощью понятия доверительной вероятности) найти возможные интервалы, изменения характеристик генеральной; совокупности (доверительные интервалы). И наоборот, рассчитать доверительную вероятность отклонения характеристики генеральной совокупности от выборочной по заданной величине доверительного интервала.
2. Найти объем планируемой выборки, позволяющей достигнуть в пределах требуемой точности расчета выборочных характеристик необходимую доверительную вероятность.
Дадим сводку необходимых для достижения этих целей формул3. Чтобы уметь применять приведенные формулы при планировании выборки в эмпирическом социологическом исследовании, познакомимся несколько подробнее с основными понятиями выборочного метода— «доверительная вероятность» и «доверительный интервал».
Теоретико-вероятностные теоремы, восходящие к закону больших чисел, позволяют с определенной вероятностью, обозначаемой (1 —а), утверждать, что для изучаемого признака отклонения выборочной средней от генеральной не превысят некоторой величины D, называемой предельной ошибкой выборки.
В одной из формулировок это утверждение записывается следующим образом:


Смысл приведенного соотношения следующий: с доверительной вероятностью (1-a) можно утверждать, что генеральное среднее лежит в интервале

который и называется доверительным интервалом, а определяет как бы степень доверия к данным, получаемым по рассчитанным с его помощью выборочным характеристикам. Отсюда и название а — уровень значимости.

Принятие того или иного уровня значимости, например 5%-ного (a = 0,05), зависит от целей данного социологического исследования, требований к степени гарантии его результатов. Социолог должен четко понимать, что, выбрав, скажем, уровень значимости, равный 5 %, и, рассчитав на основе его выборочные характеристики, мы будем утверждать наличие некоторого эффекта, который на самом деле может оказаться несправедливым приблизительно в пяти процентах случаев.
Пример. При обследовании 900 человек — лиц трудоспособного возраста — определен их средний возраст. Для вероятности (1 — a) =0,90 необходимо найти доверительный интервал, в котором содержится генеральное среднее. Поскольку дисперсия признака неизвестна, оценим ее приблизительно по значению размаха для генеральной совокупности.
С этой целью воспользуемся соотношением связи среднего квадратичного отклонения с размахом
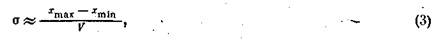
справедливым в предположении нормального характера распределения. Здесь Хmax — Хmin — вариационный размах генеральной совокупности, а V— величина, зависящая от объема выборки, значения которой можно найти в табл. 17.
Так как по всей генеральной совокупности верхняя граница трудоспособности в СССР — 60 лет, а нижняя — 16, то хmax — хmin =60—16 = 44, следовательно (для п> 100 — последний столбец

табл. 17), получим приближенное значение среднеквадратичного отклонения s=44:5= 8,8.
Величина Z находится по табл. А приложения при a/2. Таким образом, если 1 — a = 0,9, то Z = 1,64,
Подставляя найденные значения М и Z в формулу предельной ошибки, получаем D = ZM = 1,64 • 0,29 = 0,48.
Таким образом, округляя значение ошибки до половины года (0,5), можно утверждать, что с вероятностью 0,9 генеральное среднее не выйдет за пределы интервала х — 0,5 < М < х + 0,5, т. е. точность выборочной оценки среднего, рассчитанной по нашей выборке (если она организована методом простого случайного повторного отбора), оказывается равной половине года. Утверждать это мы можем с вероятностью 0,9. Интервал (х — 0,5, х + 0,5) и задает доверительный, интервагй, рассчитанный по доверительной вероятности, равной 0,9.
Теперь рассмотрим методику нахождения доверительного интервала по заданной доверительной вероятности для качественного Признака.
Пример. Выборочное обследование 900 человек, организованное до способу простого случайного повторного отбора, показало, что 18 человек не информированы о крупном событии в стране. Для Доверительной вероятности 0,95 нужно найти доверительный интервал.
Пользуясь выражением для формулы средней ошибки (см.

табл. 16)
получаем


Далее по табл. А приложения, как уже описывалось выше, для a/2 находим Z= 1,96.
Теперь можно определить величину предельной ошибки (см табл. 16):

Таким образом, доверительные границы для доли не информированных в генеральной совокупности равны 0,02 ± 0,009, или от 1,1 до 2,9%.
Приведем иллюстративный пример определения объема простой повторной случайной выборки. Как видно из формул, чтобы определить объем (см. табл. 16), для его оценки необходимо знать дисперсии генеральной средней или хотя бы ее оценки.
Для применения соответствующей формулы необходимо оценить значение дисперсии, что можно сделать (при отсутствии информации о ней и о размахе значений признака в генеральной совокупности) путем проведения одной-двух пилотажных (пробных) выборок.
Допустим, что в результате пилотажа выборочная оценка дисперсии равна 12,24. Определим каким должен быть объем выборки чтобы с вероятностью 0,95 предельное отклонение выборочной средней от генеральной не превышало одного экземпляра газет. При этих условиях получаем численность планируемой выборки

Таким образом, объем выборки должен составлять 24 человека.






