Студент должен:
знать:
- понятие вариации и ее значение;
- абсолютные и относительные показатели вариации;
уметь:
- оценить степень вариации изучаемого признака путем расчета абсолютных и относительных показателей вариации.
Вариация. Абсолютные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратичное отклонение. Способы расчета дисперсии. Относительные показатели вариации: коэффициенты осцилляции, вариации.
Методические рекомендации
Средние величины дают обобщающую характеристику совокупности по варьирующим признакам. Большое значение имеет изучение отклонений от средних.
Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Для вычисления отклонений от средней величины используют следующие показатели вариации.
1. Размах вариации вычисляется как разность между наибольшим и наименьшим значением варьирующего признака:
Размах вариации улавливает только крайние отклонения от средней, но не отражает отклонений от нее всех вариаций в ряду. Распределение отклонений можно уловить, исчислив отклонения всех вариаций от средней. А для того чтобы дать им обобщающую характеристику, необходимо далее вычислять среднюю из этих отклонений. Для этого используют ряд средних отклонений.
2. Среднее арифметическое или линейное отклонение (d) – учитывает различие всех единиц изучаемой совокупности, их колеблемость относительно среднего уровня:
3. Средний квадрат отклонение или дисперсия (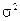
) – измеряет вариацию признака во всей совокупности под слиянием всех факторов. Чем меньше дисперсия, тем достовернее средняя отражает всю совокупность:
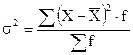
4. Среднее квадратичное отклонение (
) – обобщающая характеристика размеров вариации признака в совокупности. Говорит о типичности средней:
5. Коэффициент вариации (V) – характеристика однородности совокупности:
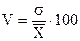
Коэффициент вариации является критерием типичности средней. Если коэффициент вариации очень большой (превышает 40%), то это означает, что средняя характеризует совокупность по признаку, который существенно изменяется у отдельных ее единиц. Типичность такой средней невелика.
Пример вычисления показателей вариации покажем на основе группировки рабочих по средней месячной выработке изделий (штук) (табл. 9).
Таблица 9
| Группы рабочих по средней месячной выработке изделий, штук | Середина интервала, Х | Число рабочих, f | 
| 
| 
| 
| 
|
| 140 – 160 | – 34 | ||||||
| 160 – 180 | – 14 | ||||||
| 180 – 200 | + 6 | ||||||
| 200 – 220 | + 26 | ||||||
| Итого | - | - | - |
1. Вычислим размах вариации:
шт.
2. Вычислим среднюю месячную выработку:
штук
3. Вычислим среднее линейное отклонение:
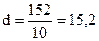штук
4. Вычислим дисперсию:
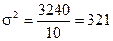
5. Вычислим среднее квадратичное отклонение:
шт.
6. Вычислим коэффициент вариации:
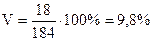
Таким образом, данная совокупность рабочих достаточно однородна по выработке, поскольку вариация признака составляет лишь 9,8%, а среднее линейное отклонение всего 15,2 штук.
Вопросы для самоконтроля
- Что представляет собой вариация признака?
- Перечислите показатели, которыми измеряется вариация признаков.
- Что такое дисперсия и как она вычисляется?
- Как вычисляется среднее квадратичное отклонение?
- Что представляет собой коэффициент вариации?
