Одной из особенностей работы лесотранспорта является постоянно возрастающее расстояние вывозки древесины, связанное с постоянным удалением мест рубок от нижнего склада. Для обеспечения работы леспромхоза в этих условиях необходимо развивать транспортные средства.
Рост грузовой работы леспромхоза можно представить уравнением прямой линии
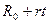 , (3.1)
, (3.1)
где R 0 - величина грузовой работы в начале рассматриваемого периода; r - прирост грузовой работы за единицу времени (год); t – число лет от начала рассматриваемого периода.
Увеличение провозной способности лесовозной дороги возможно осуществлять различными способами: приобретение дополнительных транспортных средств; переход на новые, более мощные транспортные средства; увеличение скоростей движения транспортных средств за счет реконструкции дороги и др. Каждый из этих способов требует определенных капитальных вложений. Затраты K1 какого-либо способа могут увеличить грузовую работу до величины R1, затем потребуется какой-либо другой способ, который потребует капитальных вложений K2, и т.д.
Условно будем считать, что величина капитальных вложений K пропорциональна приросту грузовой работы, а прирост грузовой работы пропорционален сроку эксплуатации дороги:  .
.
Величину капитальных вложений можно описать формулой
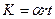 , (3.2)
, (3.2)
где 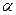 - коэффициент пропорциональности между приростом грузовой работы и капитальными затратами.
- коэффициент пропорциональности между приростом грузовой работы и капитальными затратами.
Предположим, что на лесовозной дороге можно использовать три способа увеличения провозной способности в определенной последовательности на протяжении T лет. Каждый из этих способов позволяет увеличить провозную способность на величину, зависящую от величины капитальных затрат (рис. 3.1).
Необходимо определить размеры и сроки вложения капитальных затрат, чтобы общие расходы за весь период были минимальными. В расчетах необходимо учесть экономический эффект от отдаленности капитальных вложений, приводя их к начальному году периода T.
где K1, K2, K3 – капитальные затраты соответственно 1,2,3 способов увеличения провозной способности дороги;
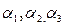 -коэффициенты пропорциональности между приростом грузовой работы и капитальными затратами при соответствующих способах; t1,t2,t3 – время (в годах) от начального периода (t0) до введения соответствующего (1,2,3) способа увеличения провозной способности дороги; T – рассматриваемый период в годах; E – нормативный коэффициент эффективности капитальных вложений.
-коэффициенты пропорциональности между приростом грузовой работы и капитальными затратами при соответствующих способах; t1,t2,t3 – время (в годах) от начального периода (t0) до введения соответствующего (1,2,3) способа увеличения провозной способности дороги; T – рассматриваемый период в годах; E – нормативный коэффициент эффективности капитальных вложений.
Провозная способность дороги увеличивается в три этапа. Требуется определить такие сроки использования капитальных вложений на каждом этапе, при которых общие приведенные затраты будут минимальными
Приведенные капитальные затраты составят
 |
 (3.3)
(3.3)
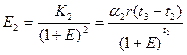 (3.4)
(3.4)
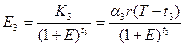 , (3.5)
, (3.5)
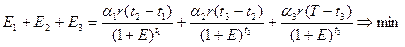 (3.6)
(3.6)
При этом необходимо учесть ограничения:
 (3.7)
(3.7)
 (3.8)
(3.8)
где R  и R
и R  – максимальные уровни провозной способности лесовозной дороги, которых можно добиться соответственно первым и вторым способом ее увеличения.
– максимальные уровни провозной способности лесовозной дороги, которых можно добиться соответственно первым и вторым способом ее увеличения.
Срок t1 определяется существующей провозной способностью Rн в начале рассматриваемого периода (см. рис. 3.1)
Rн=R0+rt1 или 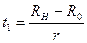 , (3.9)
, (3.9)
Уровень требуемой провозной способности в конце третьего периода также определяется однозначно по формуле
R3=R0+rT. (3.10)
Сроками капитальных вложений t2 и t3 можно варьировать, изменяя тем самым уровни провозной способности R1 и R2 первом и втором этапах. Следовательно, необходимо определить сроки t2 и t3, которые минимизируют общие приведенные капитальные затраты.
Задача решается методом динамического программирования в два этапа.
Первый этап оптимизации. Определяется значение t3 для всех возможных значений t2, которые обращают в минимум общие приведенные затраты на двух последних этапах E2+E3. Для этого исследуем на минимум функцию E2+E3 по аргументу t3.
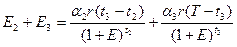 . (3.11)
. (3.11)
Продифференцируем эту функцию и приравняем нулю первую производную
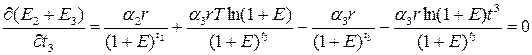 . (3.12)
. (3.12)
После преобразований получим
 . (3.13)
. (3.13)
Представим это уравнение в следующем виде
 , (3.14)
, (3.14)
где 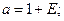
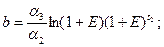
 .
.
Это уравнение типа
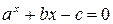 . (3.15)
. (3.15)
Решением уравнения (3.15) является общая абсцисса точки пересечения графиков двух функций (см. рис. 3.2) 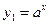 и
и 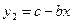 или в нашем случае
или в нашем случае  и
и  .
.
Решение может быть получено графически (рис.3.3). Для каждого возможного значения  определяются соответствующие значения
определяются соответствующие значения  , которые минимизируют суммарные приведенные затраты на втором и третьем этапах увеличения провозной способности лесовозной дороги.
, которые минимизируют суммарные приведенные затраты на втором и третьем этапах увеличения провозной способности лесовозной дороги.


y y2=c-b*x y y=c-b*t3 y=at3
y1=ax
t3
Рис. 3.2. Графическое Рис. 3.3 Графическое
решение уравнения определение значения t3
y=aх+bx-c
Второй этап оптимизации. Определяется значение 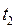 в зависимости от значения
в зависимости от значения 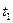 , обращающее в минимум общие приведенные затраты на всех трех этапах.
, обращающее в минимум общие приведенные затраты на всех трех этапах.
Если бы в результате первого этапа оптимизации была установлена функциональная зависимость 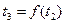 , то ее можно было бы подставить в выражение (3.6) и исследовать выражение (3.6) на минимум. Но так как зависимость
, то ее можно было бы подставить в выражение (3.6) и исследовать выражение (3.6) на минимум. Но так как зависимость 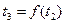 не выявлена, а установлены попарно конкретные значения
не выявлена, а установлены попарно конкретные значения 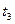 и
и 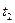 , подставим их поочередно в выражение (3.6). Значения
, подставим их поочередно в выражение (3.6). Значения 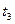 и
и 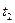 , обращающие в минимум выражение (3.6), и определяют оптимальный вариант решения задачи.
, обращающие в минимум выражение (3.6), и определяют оптимальный вариант решения задачи.






