Цель работы. Освоить методику решения задач оптимального распределения технических средств между производственными подразделениями с целью получения максимального эффекта производственной деятельности.
Задача. Распределить технологическое оборудование между производственными подразделениям для получения максимальной производительности лесопромышленного предприятия.
Часто технологическое оборудование поставляется комплектами разукомплектование которого не целесообразно. В то же время разработка лесосек может быть выполнена различными комплектами машин, но одновременное выполнение работ на одной и той же лесосеке различными бригадами вызывает большие организационные сложности и не допустимо по технике безопасности. В этом случае возникает необходимость решения задачи об оптимальном распределении технологических средств, таким образом, чтобы обеспечить максимально эффективную работу всех комплексов. Такая задача называется задачей о назначениях или задачей выбора.
РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ ВЕНГЕРСКИМ МЕТОДОМ
5.1. Описание алгоритма венгерского метода.
Введем следующие определения:
1. Нулевые элементы Z1, Z2,..., Zk квадратной матрицы С будем называть независимыми нулями, если для любого 1 ≤ i ≤ k строка и столбец, на пересечении которых лежит элемент Zi, не содержит элементов Zk для всех k≠i.
2. Две прямоугольные матрицы С = (cij) и С"= (с"ij) размером mxn назовем эквивалентными (С~С"), если с"ij = сij + αi +βj;
i =1, 2,..., m; j = 1, 2,..., n. Задачи выбора, определяемые эквивалентными матрицами, являются эквивалентными, так как можно доказать, что множества оптимальных назначений двух задач выбора с эквивалентными матрицами совпадают.
3. В процессе решения задачи некоторые строки (столбцы) матрицы С и эквивалентных ей матриц будут выделяться значком «+», стоящим справа от соответствующей строки (над соответствующим столбцом). Элементы, расположенные в выделенных строках или столбцах, будем называть выделенными элементами.
Венгерский алгоритм решения задачи о назначениях состоит из предварительного этапа и не более чем n - 2 последовательно проводимых итераций. Каждая итерация связана с эквивалентными преобразованиями матрицы, полученной в результате проведения предыдущей итерации, и с выбором максимального числа независимых нулей. Окончательным результатом итерации является увеличение числа независимых нулей на единицу. Как только  количество независимых нулей станет равным n, проблема выбора оказывается решенной: оптимальный вариант назначений определяется позициями независимых нулей в последней матрице.
количество независимых нулей станет равным n, проблема выбора оказывается решенной: оптимальный вариант назначений определяется позициями независимых нулей в последней матрице.
Предварительный этап. На этом этапе выполняются два последовательных преобразования матрицы С, в результате которых получается эквивалентная ей неотрицательная матрица С˝ в каждом столбце и каждой строке которой есть хотя бы один нуль.
Первое преобразование проделывается со всеми столбцами матрицы С. Из максимального элемента j-го столбца (i = 1, 2,..., n) вычитаются элементы этого столбца:
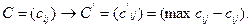
Полученная матрица С΄ является неотрицательной, и в каждом столбце этой матрицы имеется хотя бы один нуль.
Второе преобразование производится со строками матрицы С΄. Из элементов i-й строки матрицы С΄ вычитается минимальный элемент этой строки:

Если в каждой строке матрицы С' = (c΄ij), полученной после первого преобразования матрицы С, уже имеется хотя бы один нуль, то второе преобразование не производится.
В результате предварительных преобразований мы переходим от задачи выбора на максимум с матрицей С к задаче выбора на минимум с матрицей С. Наименьшее возможное значение суммы n элементов неотрицательной матрицы равно, очевидно, нулю. Следовательно, наша задача сводится к выбору в матрице C˝ (или в эквивалентной ей матрице с неотрицательными элементами) n нулевых элементов, по одному в каждой строке и каждом столбце.
Отмечаем произвольный нуль в первом столбце звездочкой (*). Затем просматриваем второй столбец, и если в нем есть нуль, расположенный в строке, где нет 0*, то отмечаем его звездочкой. Аналогично просматриваются один за другим все остальные столбцы матрицы C˝. Очевидно, что нули матрицы C˝, отмеченные звездочкой, по построению являются независимыми.
(k + 1)-я итерация
Допустим, что k-я итерация проведена и в результате получена матрица Ск. Если в матрице Ск имеется ровно n нулей со звездочкой, то процесс решения заканчивается. Если же число нулей со звездочкой меньше n, то переходим к (k + 1)-й итерации. Каждая итерация начинается первым и заканчивается вторым этапом. Между ними может несколько раз проводиться пара этапов: третий—первый. Перед началом итерации знаком «+» выделяют столбцы матрицы Сk, которые содержат нули со звездочкой.
Первый этап. Просматривают невыделенные столбцы матрицы Сk. Если среди них не окажется нулевых элементов, то переходят к третьему этапу. Если же невыделенный нуль матрицы Сk обнаружен, то возможен один из двух случаев: а) строка, содержащая невыделенный нуль, содержит также нуль со звездочкой; б) эта строка не содержит нуля со звездочкой.
В случае (а) невыделенный нуль отмечают штрихом и выделяют строку, в которой он содержится, знаком «+» справа от нее. Затем уничтожают знак «+», обводя его рамкой, над тем столбцом, на пересечении которого с данной выделенной строкой содержится нуль со звездочкой. Далее опять просматривают невыделенные столбцы, отыскивая в них невыделенные нули. Этот процесс за конечное число шагов заканчивается одним из следующих исходов:
IA — имеется невыделенный нуль в строке, где нет нуля со звездочкой. В этом случае переходят ко второму этапу, отметив последний по порядку нуль штрихом.
IB — все нули матрицы Сk выделены, т. е. находятся в выделенных строках или столбцах. При этом переходят к третьему этапу.
В случае (б), отметив невыделенный нуль штрихом, сразу переходят ко второму этапу.
Второй этап. Строят следующую цепочку из нулевых элементов матрицы Сk. отмеченный последним нуль со штрихом, нуль со звездочкой, расположенный в одном столбце с ним, нуль со штрихом, расположенный в одной строке с предшествующим нулем со звездочкой, и т. д. Итак, цепочка образуется передвижением от О' к 0* по столбцу, от 0* к 0' по строке и т. д.
Можно доказать, что описанный алгоритм построения цепочки однозначен и конечен. При этом цепочка всегда начинается и заканчивается нулем со штрихом (возможно, она будет состоять из одного нуля со штрихом). Далее, над элементами цепочки, стоящими на нечетных местах (0'), ставят звездочки, уничтожая их над четными элементами (0*). Затем уничтожают все штрихи над элементами матрицы Сk и знаки «+». При этом количество независимых нулей будет увеличено на единицу; (k+1)-я итерация закончена.
Третий этап. К этому этапу переходят после первого, если все нули матрицы Сk выделены, т. е. находятся в выделенных строках или столбцах. В таком случае среди невыделенных элементов матрицы Сk выбирают минимальный и обозначают его h > 0. Далее величину h вычитают из всех элементов матрицы Сk, расположенных в невыделенных строках, и прибавляют ко всем элементам, расположенным в выделенных столбцах. Получают новую матрицу Сk(1), эквивалентную Сk.
Поскольку среди невыделенных элементов матрицы Сk(1), появятся новые нули (согласно определению), переходят к первому этапу, при этом вместо матрицы Сk рассматривают матрицу Сk(1). Завершив первый этап, либо переходят ко второму этапу, либо вновь возвращаются к третьему этапу, если все нули матрицы Сk(1) оказываются выделенными.
После конечного числа построений очередной первый этап обязательно закончится переходом на второй этап и количество независимых нулей увеличится на единицу, т. е. (k+1)-я итерация будет завершена.
5.2. Пример решения транспортной задачи венгерским методом.
Пример 1. Имеются 5 лесопунктов и 5 комплектов лесозаготовительного оборудования (5 технологических линий). Каждая технологическая линия может дать производительность С(ij).
Выполнить: Распределить технологические линии по лесопунктам так, чтобы общая производительность была максимальной.
Решение: Венгерский алгоритм решения задачи о назначениях состоит из предварительного этапа и последовательно проводимых итераций. Каждая итерация связана с эквивалентными преобразованиями матрицы, полученной в результате проведения предыдущей итерации, и с выбором максимального числа независимых нулей. Окончательным результатом итерации является увеличение числа независимых нулей на единицу. Как только количество независимых нулей станет равным n, проблема выбора оказывается решенной: оптимальный вариант назначений определяется позициями независимых нулей в последней матрице.
Предварительный этап. На этом этапе выполняются два последовательных преобразования матрицы С, в результате которых получается эквивалентная ей неотрицательная матрица С˝ в каждом столбце и каждой строке которой есть хотя бы один нуль.
Первое преобразование проделывается со всеми столбцами матрицы С. Из максимального элемента j-го столбца (i = 1, 2,..., n) вычитаются элементы этого столбца:
Сначала находится максимальный элемент в каждом столбце: в первом столбце максимальный элемент равен 8, во втором — 7, в третьем — 7, в четвертом — 8, в пятом — 5. Из максимального элемента вычитаются элементы этого столбца. Получается неотрицательная матрица, в каждом столбце которой есть хотя бы один нуль.
Второе преобразование производится со строками матрицы С΄. Из элементов i-й строки матрицы С΄ вычитается минимальный элемент этой строки:
В результате подготовительного этапа осуществлен переход к неотрицательной матрице, в каждом столбце и каждой строке которой имеется хотя бы один нуль.
Предварительный этап (преобразование 1)
| 0* | ||||
| 0* | ||||
| 0* | ||||
| 0* |
Предварительный этап (преобразование 2)
Если в каждой строке матрицы С' = (c΄ij), полученной после первого преобразования матрицы С, уже имеется хотя бы один нуль, то второе преобразование не производится.
В результате предварительных преобразований мы переходим от задачи выбора на максимум с матрицей С к задаче выбора на минимум с матрицей С. Наименьшее возможное значение суммы n элементов неотрицательной матрицы равно, очевидно, нулю. Следовательно, наша задача сводится к выбору в матрице C˝ (или в эквивалентной ей матрице с неотрицательными элементами) n нулевых элементов, по одному в каждой строке и каждом столбце.
Отмечаем произвольный нуль в первом столбце звездочкой (*). Затем просматриваем второй столбец, и если в нем есть нуль, расположенный в строке, где нет 0*, то отмечаем его звездочкой. Аналогично просматриваются один за другим все остальные столбцы матрицы C˝. Очевидно, что нули матрицы C˝, отмеченные звездочкой, по построению являются независимыми.
В первом столбце матрицы отмечаем звездочкой нуль, расположенный в первой строке, во втором столбце — нуль в третьей строке. В третьем столбце единственный нуль находится во второй строке, отмечаем его. В четвертом столбце нуль находится во второй строке, в этой строке уже отмечен нуль в третьем столбце. В пятом столбце отмечаем звездочкой нуль в пятой строке. В результате получается четыре независимых нуля, следовательно, для решения задачи необходимо проведение одной итерации.
Каждая итерация начинается первым и заканчивается вторым этапом. Между ними может несколько раз проводиться пара этапов: третий—первый. Перед началом итерации знаком «+» выделяют столбцы матрицы Сk, которые содержат нули со звездочкой.
Итерация 1. Первый этап. Просматривают невыделенные столбцы матрицы Сk. Если среди них не окажется нулевых элементов, то переходят к третьему этапу. В нашем случае просматриваем четвертый столбец. В этом столбце имеется нуль во второй строке, значит возможен один из двух случаев: а) строка, содержащая невыделенный нуль, содержит также нуль со звездочкой; б) эта строка не содержит нуля со звездочкой. В данном примере случай (а).
В случае (а) невыделенный нуль отмечают штрихом и выделяют строку, в которой он содержится, знаком «+» справа от нее. Затем уничтожают знак «+», обводя его рамкой, над тем столбцом, на пересечении которого с данной выделенной строкой содержится нуль со звездочкой.
| + | + | + | + |
| 0* | |||||
| 0* | 0΄ | + | |||
| 0* | |||||
| 0* |
Итерация 1
Поскольку во второй строке имеется 0*, то строка подлежит выделению (ставим знак «+» справа от второй строки). Одновременно уничтожается (обводится рамкой) знак выделения над третьим столбцом, содержащим 0* во второй строке.
Далее опять просматривают невыделенные столбцы, отыскивая в них невыделенные нули. Этот процесс за конечное число шагов заканчивается одним из следующих исходов:
IA — имеется невыделенный нуль в строке, где нет нуля со звездочкой. В этом случае переходят ко второму этапу, отметив последний по порядку нуль штрихом.
IB — все нули матрицы Сk выделены, т. е. находятся в выделенных строках или столбцах. При этом переходят к третьему этапу.
В случае (б), отметив невыделенный нуль штрихом, сразу переходят ко второму этапу.
У нас имеет место случай IB, следовательно, мы переходим к третьему этапу.
Третий этап. К этому этапу переходят после первого, если все нули матрицы Сk выделены, т. е. находятся в выделенных строках или столбцах. В таком случае среди невыделенных элементов матрицы Сk выбирают минимальный и обозначают его h > 0. Далее величину h вычитают из всех элементов матрицы Сk, расположенных в невыделенных строках, и прибавляют ко всем элементам, расположенным в выделенных столбцах. Получают новую матрицу Сk(1), эквивалентную Сk.
Минимальным из числа невыделенных элементов матрицы является единица. Поэтому из всех элементов невыделенных строк (первой, третьей, четвертой, пятой) вычитаем h = 1, а к элементам выделенных столбцов (первого, второго, пятого) прибавляем h = 1. Получается матрица, эквивалентная предыдущей и содержащая незанятые нули.
| + | + | + | + |
| 0* | 0΄ | |||
| 0* | 0΄ | |||
| 0* | ||||
| 0* |
Просматриваем первый столбец и отмечаем нуль в 1 строке, во втором столбце нуль в третей строке, в третьем столбце отмечаем нуль во второй строке, в пятом столбце отмечаем нуль в пятой строке. Т.е. переносим все знаки с предыдущей матрицы. Переходим к этапу 1.
После конечного числа построений очередной первый этап обязательно закончится переходом на второй этап и количество независимых нулей увеличится на единицу, т. е. (k+1)-я итерация будет завершена.
Итерация 2. Первый этап. Перед началом итерации знаком «+» выделяют столбцы матрицы, которые содержат нули со звездочкой. Просматривают невыделенные столбцы матрицы. Если среди них не окажется нулевых элементов, то переходят к третьему этапу. Если же невыделенный нуль матрицы обнаружен, то возможен один из двух случаев: а) строка, содержащая невыделенный нуль, содержит также нуль со звездочкой; б) эта строка не содержит нуля со звездочкой.
В случае (а) невыделенный нуль отмечают штрихом и выделяют строку, в которой он содержится, знаком «+» справа от нее. Затем уничтожают знак «+», обводя его рамкой, над тем столбцом, на пересечении которого с данной выделенной строкой содержится нуль со звездочкой.
В случае (б), отметив невыделенный нуль штрихом, сразу переходят ко второму этапу.
Просматриваем невыделенные нули матрицы, четвертого столбца. Отмечаем штрихом нуль этого столбца, расположенный во второй строке. Поскольку в этой строке имеется 0*, то строка подлежит выделению (ставим знак «+» справа от второй строки). Одновременно уничтожается (обводится рамкой) знак выделения над третьим столбцом, содержащим 0* во второй строке. Рассматриваем третий столбец матрицы (так как мы сняли выделение). В этом столбце, в 1 строке имеется нуль, но в этой строке уже выделен нуль со звездочкой в 1-ом столбце. Выделяем штрихом нуль в третьем столбце, выделяем строку (ставим знак «+» справа от первой строки). Уничтожаем (обводим рамкой) знак выделения над первым столбцом, содержащим 0*.В итоге имеем три невыделенных столбца (первый, третий, четвертый)
| + | + | + | + |
| 0* | 0΄ | + | |||
| 0* | 0΄ | + | |||
| 0* | |||||
| 0΄ | |||||
| 0* |
Итерация 2
Далее опять просматривают невыделенные столбцы, отыскивая в них невыделенные нули. Этот процесс за конечное число шагов заканчивается одним из следующих исходов:
IA — имеется невыделенный нуль в строке, где нет нуля со звездочкой. В этом случае переходят ко второму этапу, отметив последний по порядку нуль штрихом.
IB — все нули матрицы Сk выделены, т. е. находятся в выделенных строках или столбцах. При этом переходят к третьему этапу.
Рассматриваем первый столбец. В этом столбце имеется невыделенный нуль в четвертой строке. В данной строке нет нуля со звездочкой. Следовательно это исход IA. В этом случае переходят ко второму этапу, отметив последний по порядку нуль штрихом.
Второй этап. Строят следующую цепочку из нулевых элементов матрицы Сk. отмеченный последним нуль со штрихом, нуль со звездочкой, расположенный в одном столбце с ним, нуль со штрихом, расположенный в одной строке с предшествующим нулем со звездочкой, и т. д. Итак, цепочка образуется передвижением от О' к 0* по столбцу, от 0* к 0' по строке и т. д.
| + | + | + | + |
 0* 0*
|  0΄ 0΄
| + | |||
 0* 0*
| 0΄ | + | |||
| 0* | |||||
| 0΄ | |||||
| 0* |
Итерация 2

Можно доказать, что описанный алгоритм построения цепочки однозначен и конечен. При этом цепочка всегда начинается и заканчивается нулем со штрихом (возможно, она будет состоять из одного нуля со штрихом). Далее, над элементами цепочки, стоящими на нечетных местах (0'), ставят звездочки, уничтожая их над четными элементами (0*). Затем уничтожают все штрихи над элементами матрицы Сk и знаки «+». При этом количество независимых нулей будет увеличено на единицу; (k+1)-я итерация закончена.
Строим цепочку. От последнего 0' (четвертая строка, первый столбец) движемся по столбцу до 0*, расположенного на пересечении первой строки и первого столбца, далее от 0* — к 0', находящемуся в этой же строке в третьем столбце. Так как в третьем столбце есть 0*, то движемся до второй строки, далее в четвертый столбец. В четвертом столбце нет 0*, процесс образования цепочки закончен.
Искомая цепочка состоит из элементов: 0'41, 0*11, 0'13, 0*23, 0'24. Снимаем звездочки у нулей из цепочки и заменяем звездочками штрихи у нулей из цепочки. В результате второй итерации число независимых нулей увеличилось на единицу и стало равно 5, поэтому процесс решения задачи закончен.
Оптимальный вариант назначений Х13 = Х24 = Х32 = Х41 = Х55 = 1. Соответствующая ему суммарная производительность 5+8+7+8+5=33
| 0* | ||||
| 0* | ||||
| 0* | ||||
| 0* | ||||
| 0* |
Результат
5.3. Алгоритм венгерского метода при определении минимальных
суммарных затрат.
Транспортная модель - это частный случай модели линейного программирования. Стандартная задача включает в себя некоторое множество пунктов производства, например, несколько лесозаготовительных предприятий, которые осуществляют поставки в некоторое множество пунктов назначения, например, в несколько деревоперерабатывающих предприятий. Цель состоит в минимизации общей стоимости транспортировки в рамках ограничений на спрос и предложение. Решение этой задачи может быть найдено с помощью традиционных методов линейного программирования. Относительно простая структура задачи позволяет, однако, разработать специальные алгоритмы, применение которых оказывается более трудоемким, чем применение обычных методов решения задач линейного программирования со множеством переменных. Для решения этой модифицированной транспортной задачи был разработан Венгерский метод.
Алгоритм венгерского метода состоит из 3 этапов:
Этап 1:
1. Формализация проблемы в виде транспортной таблицы по аналогии с решением транспортной задачи.
2. В каждой строке таблицы найти наименьший элемент и вычесть его из всех элементов данной строки.
3. Повторить ту же самую процедуру для столбцов.
Теперь в каждой строке и в каждом столбце таблицы есть по крайней мере один нулевой элемент. Представленная в полученной с помощью описанного выше приема "приведенной" транспортной таблице задача о назначениях эквивалентна исходной задаче, и оптимальное решение для обеих задач будет одним и тем же. Сущность Венгерского метода заключается в продолжении процесса приведения матрицы до тех пор, пока все подлежащие распределению единицы не попадут в клетки с нулевой стоимостью. Это означает, что итоговое значение приведенной целевой функции будет равно нулю. Так как существует ограничение на неотрицательность переменных, нулевое значение целевой функции является оптимальным.
Этап 2.
Если некоторое решение является допустимым, то каждой строке и каждому столбцу соответствует только один элемент. Если процесс распределения элементов осуществляется только в клетки с нулевой стоимостью, он приведет к получению минимального значения целевой функции.
1. Найти строку, содержащую только одно нулевое значение стоимости, и в клетку, соответствующую данному значению, поместить один элемент. Если такие строки отсутствуют, допустимо начать с любого нулевого значения стоимости.
2. Зачеркнуть оставшиеся нулевые значения данного столбца.
3. Пункты 1 и 2 повторять до тех пор, пока продолжение описанной процедуры окажется невозможным.
Если на данном этапе окажется, что есть несколько нулей, которым не соответствуют назначения и которые являются не зачеркнутыми, то необходимо:
4. Найти столбец, содержащий только одно нулевое значение, и в соответствующую клетку поместить один элемент.
5. Зачеркнуть оставшиеся нули в данной строке.
6. Повторять пункты 4 и 5 до тех пор, пока дальнейшая их реализация окажется невозможной.
Если окажется, что таблица содержит неучтенные нули, повторить операции 1-6. Если решение является допустимым, т.е. все элементы распределены в клетки, которым соответствует нулевая стоимость, то полученное решение одновременно является оптимальным. Если решение является недопустимым, осуществляется переход к этапу 3.
Этап 3.
1. Провести минимальное число прямых через строки и столбцы матрицы (но не по диагоналям) таким образом, чтобы они проходили через все нули, содержащиеся в таблице.
2. Найти наименьший среди элементов, через которые не проходит ни одна из проведенных прямых.
3. Вычесть его из всех элементов, через которые не проходят прямые.
4. Прибавить найденный элемент ко всем элементам таблицы, которые лежат на пересечении проведенных ранее прямых
5. Все элементы матрицы, через которые проходит только одна прямая, оставить без изменения.
В результате применения данной процедуры в таблице появляется по крайней мере один новый ноль. Необходимо возвратиться к этапу 2 и повторять алгоритм до тех пор, пока не будет получено оптимальное решение.
Пример 2:
Некоторое предприятие имеет 5 лесосырьевых складов и 5 потребителей лесопродукции, заказы которых необходимо выполнить. В таблице содержится расстояния между лесосырьевыми складами и потребителями. Как распределить заказы потребителям, чтобы общая дальность транспортировки была минимальной.
Этап 1Венгерского метода: В каждой строке находится наименьший элемент.
| Н.Э.строки | |||||
Наименьший элемент вычитается из всех элементов соответствующей строки
| Н.Э. столбца |
Найденный наименьший элемент вычитается из всех элементов соответствующего столбца.
Этап 2. В соответствии с процедурой, описанной в этапе 2, осуществляются назначения. Наличие назначения обозначается через 0*
| 0* | ||||
| 0* | ||||
| 0΄ | ||||
| 0* | ||||
| 0* | 0΄ |
1.Находим строку, содержащее только одно нулевое значение, и в клетку соответствующую данному значению, помещаем один элемент (строка 1, столбец 2). Если такие строки отсутствуют, то допустимо начать с любого значения нулевой стоимости.
2. Затем отметить штрихом оставшиеся нулевые значения данного столбца.
3. Пункты 1 и 2 продолжаем до тех пор, пока продолжение описанной процедуры окажется невозможным.
После выполнения пунктов 1-3 оказалось, что есть несколько нулей, которым не соответствуют назначения и которые не отмечены штрихом. Следовательно, выполняем следующие операции:
4. Находим столбец, содержащий только одно нулевое значение, и в соответствующую клетку помещаем один элемент (столбец 1, строка 5).
5. Отмечаем штрихом оставшиеся нули в данной строке (столбец 4, строка 5). Повторяем пункты 4-5 до тех пор, пока не останется неучтенных нулей.
На данном этапе мы можем осуществить только 4 нулевых назначения, тогда как требуемое их количество равно 5. Полученное распределение является недопустимым. Переходим к этапу 3.
Этап 3. Проводим наименьшее число прямых, проходящих через все нули таблицы.
 5 5
| 0* |  3 3
| ||
 4 4
| 0* | |||
| 0΄ | ||||
| 0* | ||||
 0* 0*
| 0΄ |
Наименьшим элементом, через который не проходит ни одна из прямых, является число 2. Скорректируем таблицу так, как это описано выше в соответствии с этапом 3, т.е. вычтем 2 из каждого элемента, через который не проходит ни одна прямая, и добавим 2 ко всем элементам, лежащим на пересечении трех прямых, оставив без изменения все прочие элементы, через которые проходит только одна прямая. Теперь получим:
| 0* | 0′ | |||
| 0* | ||||
| 0′ | ||||
| 0* | ||||
| 0* | 0′ |
Переходим к этапу 2 и повторяем все пункты 1-6. Получаем, опять 4 нулевых назначения, значит необходимо, повторить все операции третьего этапа

 3 3
| 0* | 0′ | ||
| 0* | ||||
| 0′ | ||||
 3 3
| 0* | |||
 0* 0*
| 0′ |
Выполнив пункты 1-6, второго этапа в конечном итоге получим:
| 0′ | 0* | |||
| 0* | 0′ | |||
| 0* | ||||
| 0* | ||||
| 0* | 0′ |
Теперь требование о размещении пяти назначений в клетки с нулевым расстоянием выполняется, следовательно, полученное решение является оптимальным. Перевозки осуществляются от базы 5 к потребителю 1, от базы 2 к потребителю 2, с базы 4 к потребителю 3, с базы 1 — к потребителю 4 и с базы 3 — к потребителю 5. Хотя данное решение и является оптимальным, однако оно не единственное.
Суммарная эффективность будет равняться 3+3+3+4+1=14
Примечание: в задачах большей размерности, чем задача из примера убедиться в том, что проведенное в соответствии с пунктом 1 этапа 3 число прямых является минимальным, гораздо труднее. В этой связи может оказаться полезным так называемое "правило правой руки":
1. Выбирается любая строка или столбец, содержащие только один нулевой элемент.
2. Если выбрана строка, прямая проводится через столбец, в котором находился данный нулевой элемент.
3. Если выбран столбец, прямая проводится через строку, содержащую данный нулевой элемент.
4. Пункты 1-3 повторяются до тех пор, пока не будут учтены все входящие в таблицу нули.
Алгоритм решения задачи о назначениях предполагает минимизацию ее целевой функции. Если имеется задача о назначениях, целевую функцию которой нужно максимизировать, то поступают таким же образом, как и в алгоритме решения транспортной задачи: после окончания формирования первой таблицы все ее элементы умножаются на (-1).




