|
Замечания
Морфологические карты предназначены для стимулирования дивергентного мышления и гарантирования того, что ни одно новое возможное решение проектной проблемы не будет упущено.
Преимущество морфологических карт! состоит в том, что для заполнения матри-1 цы требуется очень мало времени. Основ-1 ная трудность заключается в определений набора функций, которые были бы:
а) существенными для любого решения;
б) независимыми друг от друга;
I0i4 морфологические карты
I охватывающими все аспекты пробле-
1 достаточно немногочисленными, чтобы можно было составить матрицу, до- „ускающую быстрое изучение.
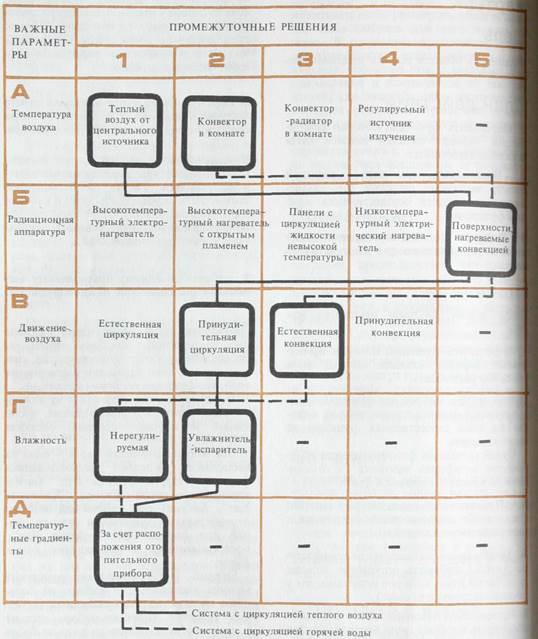
В приведенном примере A3, А4, Б5 и
П1 указывают на некоторое перекрыва-
ние 'функций. Это происходит несмотря
на то, что данный частный ряд функций
определен на основании научных исследо
ваний, а не на основе зыбкой интуиции
конструктора. При решении новых проб
лем, когда для выбора функций нельзя
опереться ни на данные исследований,
ни на практический опыт, перед проек
тировщиком стоит сложная задача уло
вить какую-то внутреннюю структуру в
том. что существует пока только в его
воображении. Способность сформулиро
вать функции в новых проектных си
туациях зависит, по-видимому, от спо
собности предвидеть полый ряд воз
можных решений и в то же время мыс
ленно расклассифицировать их. Есть ос
нования полагать, что составить морфо
логическую карту может лишь тот, кто
уже обладает иыми знаниями
или достаточным воображением, чтобы
предсказать, hi выявлено с по-
мощью карты.
Аналогичная трудность возникает и
при выборе частичных решений. Для того
чтобы общее число комбинаций было
достаточно ма я поиска, важно
оставаться на уровне широких альтер
натив, опуская незначительные вариации.
Количество Ki чень быстро
возрастает по величения коли-
чества функци! гичных решений;
например, матрица 10X10 уже дает 1Г' млрд комбинаций.
Недостат(i i состой
Т"М. что как для выявления функций.
так и для поиска приемлемых комби
наций частичных решений требуется зна-
груктуры npi
; не раскрыв преимущест-
во в том, что он заставляет проектировщика расширить область поиска.
Применение
Этот метод достаточно успешно применялся для поиска решений ряда новых инженерных проблем самого различного характера - от транспортировки нефти без танкеров до конструкции быстро убираемого навеса от дождя над площадкой для игры в крикет. Наилучшие результаты он, по-видимому, может дать при исследовании ограниченных областей поиска, а не при изучении плохо определенных и нечетко сформулированных проблем.
Обучение
Студенты-выпускники проектных специальностей, работавшие по этому методу, испытывали значительные трудности при формулировании функций. Опытные проектировщики в области машиностроения и строительной техники быстро научились пользоваться этим методом, успешно и охотно применяя его в областях, где структура проблемы им более или менее знакома и они имеют представление о практической осуществимости тех или иных решений.
Стоимость и время
На выявление функций и составление матрицы требуется всего несколько часов. Исчерпывающий поиск для нахождения всех наборов частичных решений требует более длительного времени. Дальнейший поиск обычно прекращается, как только выявляется несколько практически полезных комбинаций.
Библиография
Норрис [103].Цвикки [104].
Гл ава 11____________
