„тобы найти коллективное предпочтение, требуетс€ каким- то образом объединить, а зачастую и согласовать друг с другом индивидуальные предпочтени€ членов ѕ–. ƒл€ взаимного учета индивидуальных интересов устанавливаетс€ некоторый принцип согласовани€, который позвол€ет выделить наилучшие с коллективной точки зрени€ варианты. ”кажем наиболее известные принципы согласовани€ интересов участников при кол≠лективном выборе (см. табл. 1).
- ѕринцип урно. ¬се члены ѕ– имеют различные соб≠ственные интересы и делают свой выбор независимо друг от друга, т. е. число коалиций равно числу членов ѕ–. “огда никакому участнику по отдельности не выгодно мен€ть свое предпочтение, так как это может только ухудшить прин€тое решение.
- ѕринцип ѕарето. ¬се члены ѕ– имеют общие интересы и делают свой выбор согласованно, т. е. имеетс€ одна-единственна€ коалици€. “огда всем участникам вместе не выгодно мен€ть свои предпочтени€, так как это может только ухудшить прин€тое решение.
- ѕринцип Ёджворта. ¬се члены ѕ– вход€т в коалиции, число которых может быть любым (от одного до равного числу членов ѕ–), и делают свой выбор в интересах своей коалиции. “огда никакой коалиции не выгодно мен€ть свои предпочтени€, так как это может только ухудшить прин€тое решение.
ѕарадокс ондорсе́ Ч парадокс теории общественного выбора, впервые описан маркизом ондорсе в 1785 г.
ќн заключаетс€ в том, что при наличии более двух альтернатив и более двух избирателей коллективна€ ранжировка альтернатив может быть цикличной (не транзитивна), даже если ранжировки всех избирателей не €вл€ютс€ цикличными (транзитивны). “аким образом, волеизъ€влени€ разных групп избирателей, кажда€ из которых представл€ет большинство, могут вступать в парадоксальное противоречие друг с другом.
ќбобщЄн теоремой Ђо невозможностиї Ёрроу в 1951 г.
Ќа практике иде€ о необходимости ранжировани€ кандидатов реализована в голосовании по методу Ўульце.
ѕринцип ондорсе
ондорсе определил правило, по которому сравнение выбираемых альтернатив (кандидатов) производитс€ с учетом полной ординалисткой информации о предпочтени€х избирателей.
—огласно принципу ондорсе, дл€ определени€ истинной воли большинства необходимо, чтобы каждый голосующий проранжировал всех кандидатов в пор€дке их предпочтени€. ѕосле этого дл€ каждой пары кандидатов определ€етс€, сколько голосующих предпочитает одного кандидата другому - формируетс€ полна€ матрица попарных предпочтений избирателей.
Ќа базе этой матрицы, использу€ транзитивность отношени€ предпочтени€, можно попытатьс€ построить коллективную ранжировку кандидатов
ѕример применени€ принципа
ѕриведЄм численный пример из работы ондорсе.
¬ведЄм дл€ краткости обозначение:  будет означать, что голосующий предпочитает кандидата A кандидату B, а кандидата B Ч кандидату —.
будет означать, что голосующий предпочитает кандидата A кандидату B, а кандидата B Ч кандидату —.
ѕусть 60 голосующих дали следующие предпочтени€:
23 человека: 
19 человек: 
16 человек: 
2 человека: 
ѕри сравнении A с B имеем: 23 + 2 = 25 человек за то, что  , и 19 + 16 = 35 человек за то, что
, и 19 + 16 = 35 человек за то, что  . ѕо принципу ондорсе мнение большинства состоит в том, что ¬ лучше ј.
. ѕо принципу ондорсе мнение большинства состоит в том, что ¬ лучше ј.
|
|
|
—равнива€ ј и —, будем иметь: 23 человека за  и 37 человек за
и 37 человек за  . ќтсюда, по ондорсе, заключаем, что большинство предпочитает кандидата — кандидату ј. јналогично (19 человек за
. ќтсюда, по ондорсе, заключаем, что большинство предпочитает кандидата — кандидату ј. јналогично (19 человек за  , 41 человек за
, 41 человек за 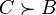 ) — более предпочтителен, чем B.
) — более предпочтителен, чем B.
“аким образом, по ондорсе вол€ большинства выражаетс€ в виде трех суждений: 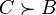 ;
;  ;
;  , которые можно объединить в одно отношение предпочтени€ C > B > A и если необходимо выбрать одного из кандидатов, то, согласно принципу ондорсе, следует предпочесть кандидата —.
, которые можно объединить в одно отношение предпочтени€ C > B > A и если необходимо выбрать одного из кандидатов, то, согласно принципу ондорсе, следует предпочесть кандидата —.
ѕротиворечие с мажоритарной системой голосовани€
—равним этот вывод с возможным исходом голосовани€ по мажоритарной системе относительного или абсолютного большинства.
ƒл€ вышеприведенного примера голосование по системе относительного большинства даст такие результаты: за ј Ч 23 человека, за ¬ Ч 19 человек, за — Ч 18 человек. “аким образом, в этом случае победит кандидат ј.
ѕри голосовании по системе абсолютного большинства кандидаты ј и ¬ выйдут во второй тур, где кандидат ј получит 25 голосов, а кандидат ¬ Ч 35 голосов Ч и победит.
ѕолучаем, что правила игры будут определ€ть победител€, и эти победители будут разными при различных правилах голосовани€. —огласно второй, широко используемой в мире процедуре победить может кандидат, который проигрывает отсе€нному в первом туре кандидату в отношении вплоть до 1 к 1,99... ѕарадоксальность такой ситуации на реальных выборах иногда путают собственно с парадоксом ондорсе.[1] ѕринцип ондорсе устран€ет подобные ошибки, св€занные с неполным учетом предпочтений избирателей в первом туре, но может приводить к неразрешимому противоречию
¬ другом примере, рассмотренном ондорсе:
- 1 человек:

- 1 человек:

- 1 человек:

по итогам голосовани€ двум€ трет€ми голосов получаем три утверждени€:  ,
,  ,
,  . Ќо вместе эти утверждени€ противоречивы. ¬ этом и состоит парадокс ондорсе или парадокс коллективного выбора. ќказываетс€ невозможным определить волю большинства и прин€ть какое-то согласованное решение.
. Ќо вместе эти утверждени€ противоречивы. ¬ этом и состоит парадокс ондорсе или парадокс коллективного выбора. ќказываетс€ невозможным определить волю большинства и прин€ть какое-то согласованное решение.
¬ силу симметрии в таком виде парадокс неразрешим никакими ухищрени€ми. Ќо если заменить отдельных избирателей в этом примере на три группы с близким, но не одинаковым числом избирателей, например, 9, 10 и 11, то метод Ўульце позвол€ет формально определить победител€. ’от€ парадоксальна€ цикличность коллективной ранжировки сохран€етс€.
ѕарадокс составного голосовани€
¬ другой форме парадокс ондорсе возникает при постатейном прин€тии некоторого постановлени€ или закона, когда кажда€ из статей закона принимаетс€ большинством голосов, а поставленный на голосование закон в целом отвергаетс€ (иногда даже стопроцентным большинством голосующих). Ћибо наоборот, вполне возможно, что коллективно будут прин€ты решени€, которые на индивидуальном уровне не поддерживал ни один из голосующих.
ѕример. ѕусть у нас имеютс€ три человека, голосующих по трем вопросам. ѕервый из них голосует Ђдаї по первому вопросу, Ђдаї по второму и Ђнетї по третьему (Ђдаї/Ђдаї/Ђнетї), второй Ч Ђдаї/Ђнетї/Ђдаї, третий Ч Ђнетї/Ђдаї/Ђдаї. —уммарный итог голосовани€ подсчитываетс€ как соотношение сумм голосов Ђдаї и Ђнетї по каждому из вопросов. ¬ рассмотренном случае суммарный итог голосовани€ будет Ђдаї/Ђдаї/Ђдаї. Ётот итог не отражает мнени€ ни одного из голосовавших и, естественно, не удовлетвор€ет никого.
јльтернативное голосование
|
|
|
Ќа практике иде€ ондорсе о необходимости ранжировани€ кандидатов реализована в альтернативном голосовании. ƒанный метод примен€етс€ при выборах в различные органы власти јвстралии, Ќовой «еландии, ѕапуа Ч Ќовой √винеи, ‘иджи, »рландии, —Ўј, а также в р€де политических партий, неправительственных организаций и т. д.






