ќсновные пон€ти€ теории игр. ¬ведение в матричные игры
ѕрин€тие решений в проблемных ситуаци€х в услови€х неопределенности €вл€етс€ одним из важнейших аспектов различных областей жизни и трудовой де€тельности людей (в области экономики, военного дела, торговли, транспорта, экологии и других). —итуации, в которых присутствует неопределенность и эффективность принимаемого одной стороной решени€ зависит от действий другой стороны, называютс€ конфликтными. ¬ процессе прин€ти€ решений в услови€х неопределенности и конфликта (разногласий) сторон часто используютс€ игровые модели. ¬ услови€х неопределенности и риска обоснование решений на основе применени€ математической модели может повысить веро€тность успеха.
ѕредметом исследований в теории игр €вл€ютс€ модели и методы прин€ти€ решений в ситуаци€х, где участвуют несколько сторон (игроков), при этом цели игроков различны, часто противоположны.
“еори€ игр впервые была систематически изложена ƒж. фон Ќейманом и ќ. ћоргенштерном в 1944 г., хот€ отдельные результаты были опубликованы еще в 20-х годах. Ќейман и ћоргенштерн рассматривали модели игры как средство математического подхода к €влени€м конкурентной экономики.
ћатематическа€ модель игровых ситуаций называетс€ игрой. ¬ игре участвует множество действующих субъектов, называемых коалици€ми действи€, или игроками. ¬ зависимости от числа участников игры подраздел€ютс€ на парные и множественные. ¬ парной игре число участников равно двум, в множественной Ц более двух. ”частники множественной игры могут образовывать коалиции, в этом случае игры называютс€ коалиционными. онфликтна€ ситуаци€ будет антагонистической, если увеличение выигрыша одной из сторон на некоторую величину приведет к уменьшению выигрыша другой стороны на такую же величину, и наоборот. “аким образом, под антагонистической игрой понимаетс€ взаимодействие двух субъектов (организаций, фирм, стран) с противоположными интересами.
»гра состоит из последовательности ходов. ’одом называетс€ выбор игроком одного из предусмотренных правилами игры действий и его осуществление. ’оды бывают личные (игрок сознательно выбирает и осуществл€ет определенный вариант действий) и случайные (выбор осуществл€етс€ с помощью какого-то механизма случайного выбора). –ешение, принимаемое игроком при личном ходе, называетс€ выбором, при случайном ходе Ц исходом.
–езультаты ходов оцениваютс€ функцией выигрыша дл€ каждого игрока. ≈сли сумма выигрышей равна 0, то игра называетс€ игрой с нулевой суммой, то есть выигрыш одного игрока равен проигрышу другого.
—тратегией называетс€ набор правил, определ€ющих поведение игрока, т.е. выбор хода. ажда€ фиксированна€ стратеги€, которую может выбрать игрок, называетс€ его чистой стратегией. —тратеги€, заключающа€с€ в выборе с определенной частотой (веро€тностью) чистых стратегий, называетс€ смешанной стратегией. »гра называетс€ конечной, если число стратегий игроков конечно, и бесконечной, если хот€ бы у одного из игроков число стратегий €вл€етс€ бесконечным.
|
|
|
ќптимальной стратегией называют такую стратегию, при которой достигаетс€ максимальный ожидаемый средний выигрыш игрока или минимально возможный средний проигрыш (независимо от поведени€ противника) при многократном повторении игры.
÷ель теории игр Ц оптимизаци€ поведени€ игрока в игре, где нар€ду со случайными ходами есть и личные.
ћатричные игры Ч это игры, где два игрока играют в игру с нулевой суммой, име€ конечное число Ђчистыхї стратегий: {1,Е, m } и {1,Е, n } и "(ij) задан платеж aij второго игрока первому. ћатрица (aij) задает выигрыш первого игрока и проигрыш второго.
»спользу€ пон€тие стратегии, любую игру можно рассматривать следующим образом: каждый игрок имеет один ход Ц выбор между своими стратеги€ми из некоторого множества доступных ему стратегий. ѕри этом в общем случае каждый игрок принимает решение, не име€ никакой информации о выборе других игроков.
ƒл€ игр с одной коалицией действи€ множество всех ситуаций можно прин€ть за множество стратегий этой коалиции действи€ и далее о стратеги€х не упоминать; такие игры называютс€ нестратегическими. ¬ажным классом таких игр €вл€ютс€ игры с природой, примен€емые дл€ анализа экономических ситуаций, оценки эффективности принимаемых решений и выбора наиболее предпочтительных альтернатив, в которых риск св€зан с совокупностью неопределенных факторов окружающей среды, именуемых Ђприродаї.
“аким образом, различные виды игр можно классифицировать, основыва€сь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействи€ между игроками в ходе игры.
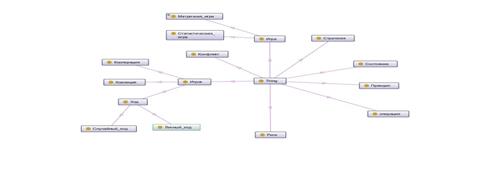
–ис. 3.1Ц ‘рагмент онтологии теории игр






