Эвольвента окружности – это кривая, центры кривизны которой лежат на окружности. Эвольвенту окружности 
(рис. 2), которую описывает точка 
прямой 
, можно получить, если прямую перекатыватьбез скольженияпо окружности радиуса 
. Эта окружность называется основной.
Основные свойства эвольвенты:
а) радиус кривизны в произвольной точке равен 
и, следовательно, центр кривизны любой точки эвольвенты лежит на основной окружности;
б) радиус кривизны нормален к эвольвенте в точке и касается основной окружности в точке 
;
в) длина касательной равна длине дуги 
;
г) эвольвента не имеет точек внутри основной окружности.
Рис. 2
Уравнения эвольвенты в параметрической форме (параметр угол 
, рис. 2) имеют вид:
, 
.
Функцию 
называют эвольвентной функцией и сокращенно пишут 
(инволюта ) т.е.
.
4. Эвольвентное зацепление и его свойства
В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении.
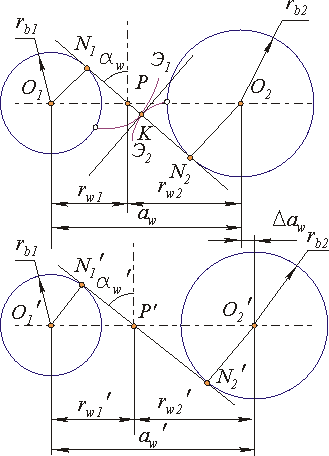
Рис. 3
Свойство 1. Передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной:
Свойство 2. При изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется.
Свойство 3. При изменении межосевого расстояния в эвольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.
Свойство 4. За пределами отрезка линии зацепления N1N2 рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили, выполненные по этим кривым, будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.
5. Геометрические параметры эвольвентного зубчатого колеса
Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. Основные геометрические параметры эвольвентного зубчатого колеса показаны на рис. 4. В инженерных расчетах для определения геометрических размеров зубчатых колес используется некоторый параметр, называемый модулем зацепления.
|
Рис. 4
Модулем зацепления называется линейная величина в p раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p: 
.
Модуль можно определить как число миллиметров диаметра, приходящееся на один зуб. В зависимости от окружности, по которой определен модуль, различают делительный, основной, начальный. ГОСТом введен стандартный ряд модулей. Стандартный модуль определяется по окружности, называемой делительной.
Делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Делительная окружность делит зуб на головку и ножку. Радиус делительной окружности согласно ГОСТ обозначается r.
Окружность вершин (ra) - очерчиваетвершины зубьев.
Окружность впадин (rf) - очерчивает ножки зубьев.
Основная окружноcть (rb) – это окружность, по которой перекатывается нормаль .
Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба).
Угловой шаг t - центральный угол, соответствующий дуге p - окружному шагу.
Углом профиля a называется острый угол между касательной к профилю в данной точке и радиусом - вектором, проведенным в данную точку из центра колеса.
Шаг колеса делится на толщину зуба sy и ширину впадины ey.
Толщина зуба s y - расстояние по дуге окружности ry между разноименными точками профилей зуба.
Ширина впадины ey - расстояние по дуге окружности r y между разноименными точками профилей соседних зубьев.
В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на: нулевые s = e
положительные s > e; отрицательные s < e.
