Второго порядка
Дифференциальным уравнение второго порядка называется соотношение вида
.
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные
.
Наиболее простыми из дифференциальных уравнений второго порядка являются уравнения, разрешенные относительно второй производной и имеющие вид
.
Их решение находят двукратным интегрированием:
,
.
Пример. Решить уравнение 
.
Решение. Находим
,
.
Дифференциальные уравнения
Второго порядка
С постоянными коэффициентами
Линейным однородным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где 
и 
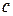– постоянные величины.
Для нахождения общего решения однородного уравнения составляется характеристическое уравнение
.
Структура общего решения однородного уравнения зависит от характера корней:
§ если корни вещественные, различные, т.е. 
, то общее решение уравнения имеет вид:
§ если корни вещественные, кратные, т.е.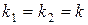 
, то общее решение уравнения имеет вид:
§ если корни комплексные, т.е. 
, то общее решение уравнения имеет вид
Пример. Решить уравнение 
.
Решение. Ему соответствует характеристическое уравнение 
, корнями которого являются 
. Следовательно, общее решение однородного уравнения имеет вид
.
Пример. Решить уравнение 
.
Решение. Ему соответствует характеристическое уравнение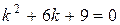 
. Найдем его корни:
.
Корни вещественные кратные, т.е. 
, Следовательно, общее решение уравнения имеет вид:
.
Пример. Решить уравнение 
.
Решение. Ему соответствует характеристическое уравнение 
. Найдем его корни:
.
Действительная часть 
, мнимая часть 
. Следовательно, общее решение однородного уравнения имеет вид
.
| 8. Числовые ряды |
Рядом называется сумма бесконечного множества слагаемых
являющихся членами бесконечной последовательности.
Числа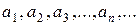 
называются членами ряда.
Сумма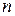 
первых членов ряда называется 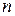-ой частичной суммой.
.
Ряд называется сходящимся, если последовательность его частичных сумм при 
имеет конечный предел:
Этот предел называется суммой сходящегося ряда.
Если 
не существует или бесконечен, то ряд называется расходящимся.
Пример. Написать 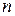-ый член ряда по данным первым его членам.
1. 
Ответ: 
.
2. 
Ответ: 
.
3. 
Ответ: 
.
Необходимый признак
Сходимости числового ряда
Если ряд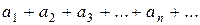 
сходится, то его общий член 
при , т.е.
.
! Этот общий признак не является достаточным, т.е. из того, что общий член стремиться к нулю при , нельзя сделать вывод о сходимости ряда. Но если общий член не стремится к нулю, то ряд расходится.
Пример. Исследовать на сходимость ряд 
Решение. Проверим, выполняется ли необходимое условие сходимости ряда, а именно . В наше случае 
, тогда
.
Так как необходимое условие не выполняется, то этот ряд расходится.
Ряд, членами которого являются только положительные числа, называется знакоположительным.
