Этот тип уравнения является самым простым типом уравнений первого порядка.
Дифференциальное уравнение вида

называется уравнением с разделяющимися переменными.
Представим производную как отношение дифференциалов  , тогда
, тогда
 .
.
Умножаем на 
 .
.
Разделение переменных производится делением обеих частей последнего соотношения на произведение  , в котором
, в котором  ,
,  . После деления уравнение примет вид
. После деления уравнение примет вид
 или
или  ,
,
а его общий интеграл запишется так:
 или
или  .
.
Пример. Решить уравнение  .
.
Решение. Подставим вместо 
 .
.  .
.
Разделим на 
 .
.
Интегрируя, получим
 .
.
Здесь удобно представить константу в логарифмической форме. Из последнего равенства получим
 ;
;  .
.
Однородные дифференциальные уравнения
Первого порядка
Функция  называется однородной степени
называется однородной степени  , если для нее выполняется равенство
, если для нее выполняется равенство
 .
.
Однородными функция будут:
 – вторая степень однородности
– вторая степень однородности
 – вторая степень однородности
– вторая степень однородности
 – первая степень однородности
– первая степень однородности
 – нулевая степень однородности
– нулевая степень однородности
Неоднородные функции:  ,
,  ,
,  .
.
Однородным дифференциальным уравнением первого порядка называют соотношение вида
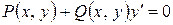 ,
,
где 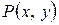 и
и  – однородные функции одинаковой степени однородности.
– однородные функции одинаковой степени однородности.
Дифференциальное уравнение может быть представлено в виде
 .
.
Для решения однородных дифференциальных уравнений первого порядка применяют подстановку
 ,
,
где  – новая искомая функция, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
– новая искомая функция, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
После того как новое уравнение будет проинтегрировано, следует  заменить на
заменить на  .
.
Пример. Решить уравнение 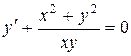 .
.
Решение. Убедимся, что это уравнение однородное. Заменить 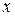 на
на  , а
, а 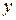 на
на  , видим, что уравнение не изменилось это и доказывает, что оно однородное.
, видим, что уравнение не изменилось это и доказывает, что оно однородное.
Сделаем подстановку:
 , откуда
, откуда  ,
,
и уравнение перепишется так:
 ,
,
 ,
,
 ,
,
 .
.
Теперь мы получили уравнение с разделяющимися переменными, которое после разделения переменных запишется следующим образом:
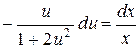 .
.
Интегрируя, получаем:

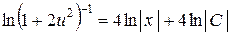 , или
, или 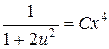 .
.
Заменяя  на
на  , получим
, получим
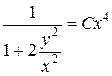 ;
;
 ;
;  .
.
7.3. Линейные дифференциальные уравнения
первого порядка
Дифференциальные уравнения вида

называются линейными потому, что искомая функция 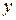 и ее производная
и ее производная  входят в уравнение в первой степени.
входят в уравнение в первой степени.
Функции  и
и  предполагаются непрерывными в промежутке
предполагаются непрерывными в промежутке  , в котором ищется решение уравнения.
, в котором ищется решение уравнения.
Линейное дифференциальное уравнение первого порядка при помощи подстановки  сводится к двум уравнениям с разделяющимися переменными.
сводится к двум уравнениям с разделяющимися переменными.
Пример. Решить уравнение 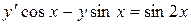 .
.
Решение. Запишем уравнение в виде:  .
.
Разделяя на 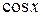 , получим:
, получим:  .
.
Полагаем  , тогда
, тогда  и данное уравнение примет вид:
и данное уравнение примет вид:
 ,
,
или
 .
.
Решаем уравнение
 ,
,
находим его простейшее решение
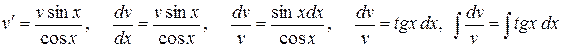 ,
,
откуда
 ;
;  .
.
Подставляя  в уравнение
в уравнение  , получим уравнение
, получим уравнение
 , откуда
, откуда  ,
,
 ,
,
 ,
,  .
.
Значит, искомое общее решение можно записать в виде:
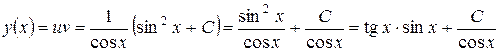 .
.






