Для отыскание предела некоторых тригонометрических функций применяется правило: предел отношения синуса к своему аргументу при 
равен единице
.
Часто применяют формулу 
.
Пример. Найти
1) 
. 2) 
.
Решение. На основании приведенного выше правила имеем:
1) 
.
2) 
.
Второй замечательный предел
В случае возникновения неопределенности вида 
применяют второй замечательный предел:
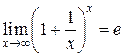
Число 
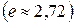широко применяют в математике. В частности, число берут в качестве основания логарифма. Такие логарифмы называют натуральными: 
.
Пример. Вычислить 
.
Решение. Чтобы вычислить этот предел с помощью второго замечательного предела необходимо сначала выделить единицу
.
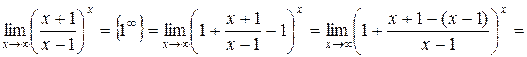
| 2. Производная функции |
Понятие производной функции
Рассмотрим функцию 
. На кривой (рис. 3) возьмем произвольную точку 
с абсциссой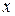 
. Придадим 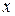приращение 
. Новому значению 
соответствует точка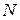 
кривой. При этом функция получит приращение
.
  
 
 
 
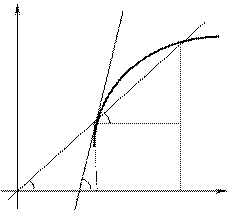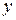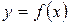
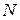
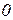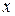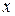Рис. 3
| Отношение 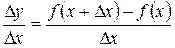 показывает, во сколько раз “в среднем” приращение функции больше (или меньше) приращения ее аргумента. Это отношение называют средней скоростью изменения функции  на участке . Чем меньше , тем лучше средняя скорость на участке
|
будет характеризовать ту скорость, с которой меняется функция в точке 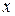. Поэтому за мгновенную скорость изменения функции в точке 
естественно принять
.
Этот предел и называется производной.
| Определение. | Производной функции  в точке 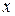называется предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю:
 .
|
Производная представляет собой скорость изменения функции в точке 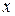, т.е. скорость, с которой изменяется функция при переходе через точку. Таков наиболее общий смысл производной.
Геометрический смысл производной. Производная в точке 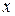равна тангенсу угла наклона касательной к кривой в точке , т.е. угловому коэффициенту касательной.
В теоретическом плане подчеркнем, что существование предела, которым выражается производная, надо понимать в общем смысле существования предела функции в точке. Это означает, что 
должен существовать не только при 
, но и при 
, причём оба предела должны совпадать. В этом требовании и заключается условие существования производной в точке 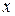. С геометрической точки зрения это условие означает независимость предельного положения секущей от выбора точки справа или слева от точки .
Функция, имеющая производную, называется дифференцируемой.
Таблица производных
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
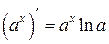
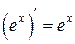
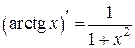
Формулы дифференцирования
Если функции 
и 
дифференцируемы в точке 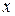, то в точке 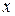дифференцируемы функции 
, 
, 
, 
, 
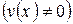и справедливы формулы:
§ 
;
§ 
;
§ 
;
§ 
.
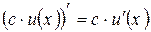