МАТЕМАТИКА ДЛЯ ЕКОНОМІСТІВ
(вища математика)
Курс лекцій
для студентів економічних спеціальностей
(ФІН, ОА, БС, ЕП, МЕ)
Автори: Щетініна О.К., Шепеленко О.В.,
Фоміна Т.О., Скрипник С.В., Латинін С.М, Фортуна В.В.
ЗМІСТ
| Елементи лінійної алгебри та аналітичної геометрії... | |
| Лекція 1. Визначники та матриці | |
| 1.1. Визначники…………………………................................................. | |
| 1.2. Матриці……………………………………………………………… | |
| 1.3. Обернена матриця………………………………………………… | |
| Лекція 2. Системи лінійних рівнянь……………………………………… | |
| 2.1. Формули Крамера…………………………………………………. | |
| 2.2. Метод оберненої матриці………………………………………… | |
| 2.3. Метод Гаусса………………………………………………………... | |
| Лекція 3. Елементи векторної алгебри…………………………………… | |
| 3.1. Лінійні операції з векторами…………………………………….. | |
| Лекція 4. Аналітична геометрія на площині………………………… | |
| 4.1. Довжина відрізку та ділення відрізка ……………………….….. | |
| 4.2. Рівняння прямої……………………………………………………. | |
| 4.3. Криві другого порядку…………………………………………….. | |
| Границі і диференціальне числення функцій ………… | |
| Лекція 5. Границі і неперервність……………………………………… | |
| 5.1. Означення границі………………………………………………… | |
| 5.2. Границя функції…………………………………………………… | |
| 5.3. Визначні границі…………………………………………………… | |
| 5.4. Неперервність функції……………………………………………. | |
| Лекція 6. Похідна і диференціал………………………………………… | |
| 6.1. Означення похідної. Необхідна умова диференційовності функції……………………………………………………………… | |
| 6.2. Основні формули та правила диференціювання…………… | |
| 6.3. Неявна функція та її диференціювання………………………. | |
| 6.4. Логарифмічне диференціювання……………………………… | |
| 6.5. Похідні вищих порядків…………………………………………. | |
| 6.6. Диференціал……………………………………………………….. | |
| Лекція 7. Дослідження функцій і побудова графіків……………….. | |
| 7.1. Інтервали монотонності і екстремум функції……………….. | |
| 7.2. Опуклість і угнутість графіка функції. Точки перегину….. | |
| 7.3. Асимптоти кривої……………………………………………….... | |
| 7.4. Загальна схема дослідження функції…………………………. | |
| Лекція 8. Функції багатьох змінних……………………………………………….. | |
| 4.1. Частинні похідні і повний диференціал………………………. | |
| 8.2 Екстремум функції двох змінних……………………………….. | |
| Інтегральне числення.……………………………………... | |
| Лекція 9. Невизначений інтеграл…………………………………….. | |
| 9.1. Поняття невизначеного інтеграла………………………………. | |
| 9.2. Таблиця основних інтегралів……………………………………. | |
| 9.3. Безпосереднє інтегрування……………………………………… | |
| 9.4. Метод заміни змінної (метод підстановки)…..……………….. | |
| 9.5. Інтегрування частинами…………………………………………. | |
| 9.6. Інтеграли від деяких виразів з квадратним тричленом……... | |
| 9.7. Інтеграли від деяких ірраціональних функцій……………….. | |
| 9.8. Інтегрування деяких класів тригонометричних функцій…. | |
| Лекція 10. Визначений інтеграл…………………………………………… | |
| 10.1. Основні поняття………………………………………………….... | |
| 10.1. Методи обчислення визначеного інтеграла…..……….... | |
| Лекція 11. Застосування визначеного інтеграла……………………….. | |
| 11.1. Обчислення площ плоских фігур…………………………….. | |
| Лекція 12. Невласні інтеграли………………………………………….. | |
| 12.1. Невласні інтеграли першого роду………………………………. | |
| 12.2. Невласні інтеграли другого роду………………………….. | |
| Диференціальні рівняння. Ряди. …….…………………. | |
| Лекція 13. Звичайні диференціальні рівняння………………………… | |
| 13.1. Основні поняття………………………………………………… | |
| 13.2. Диференціальні рівняння з відокремлюваними змінними. | |
| 13.3. Однорідні диференціальні рівняння……………………... | |
| 13.4. Лінійні диференціальні рівняння………………………… | |
| 13.5. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами…………………………… | |
| Лекція 14. Ряди……………………………………………………………...... | |
| 14.1. Поняття числового ряду. Сума ряду………………………… | |
| 14.2. Збіжність числових рядів. Необхідна ознака………………. | |
| 14.3. Достатні ознаки збіжності……………………………………….. | |
| 14.4. Знакопочергові ряди…………………………………………… | |
| 14.5. Степеневі ряди………………………………………………… | |
| 14.6. Формула Тейлора……………………………………………….. | |
| 14.7. Використання рядів у наближених обчисленнях……….. |
ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ І АНАЛІТИЧНОЇ ГЕОМЕТРІЇ.
Лекція 1. Визначники та матриці
Предметом розгляду лінійної алгебри для економістів є насамперед теорія систем лінійних рівнянь, які в загальному вигляді можна подати так:
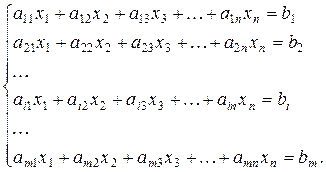(1.1)
Система (1.1) називається системою m лінійних рівнянь з n невідомими (змінними), де x 1, x 2,..., xn — невідомі; aij 
— коефіцієнти системи рівнянь; bi 
— вільні члени, або праві частини системи рівнянь. Якщо всі bi = 0 , то система лінійних рівнянь називається однорідною.
Розв’язком системи рівнянь (1.1) є множина таких чисел k 1, k 2, ..., kn, у результаті підставляння яких замість відповідних невідомих x 1, x 2, ..., xn у кожне з рівнянь системи (1.1) останні перетворюються на правильні числові рівності.
Якщо система рівнянь не має жодного розв’язку, вона називається несумісною, а якщо має хоча б один розв’язок — сумісною. Сумісна система рівнянь називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо розв’язків більш як один.
Визначники
визначник порядкуn (детермінант) А - це число, або алгебраїчний вираз записані у вигляді квадратної таблиці чисел або алгебраїчних виразів, що має n рядків і n стовпців. Записується визначник як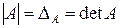 
.
